While genuinely addressing the core issue of blockchain scalability, that is to say finding a remedy for the challenge where every node is required to process every transaction, is an extremely complex task, various proposed fixes that enhance performance relative to Bitcoin’s methods can actually be quite simple to identify. For instance, in Ethereum, there exists the notion of a distinct state tree and transaction record, permitting miners to easily retain only the current account states and avoid historical transaction outputs that have become irrelevant, therefore significantly minimizing required storage; if Bitcoin serves as a reference point, the savings should approximate 90%. A further enhancement is the utilization of accounts rather than coins/UTXO as the primary unit, enabling each user to occupy less than a hundred bytes on the blockchain, regardless of the volume of transactions to and from their account. Naturally, both of these improvements are somewhat, or perhaps even entirely, counteracted by Ethereum’s broader ambitions, which aim to leverage the blockchain for purposes beyond mere financial transactions. Yet, if this holds true, it emphasizes the pressing need for scalability even more. What I am planning to elucidate in this article is another strategy to combat bloat that may yield very significant benefits, targeting this time the issue of “dust”.
Dust, in basic terms, signifies the build-up of minuscule outputs (or accounts) on the blockchain, potentially holding only a minuscule fraction of a cent’s worth of cryptocurrency, which are either maliciously introduced onto the blockchain or simply too low in value to justify the increased transaction fee for transmission. In Ethereum, the latter type of dust may also comprise accounts that have a zero balance, possibly due to users wishing to switch to a different private key for safety purposes. Dust presents a significant challenge; estimates suggest that a substantial portion of the Bitcoin blockchain comprises dust, and in Litecoin, approximately 90% of the outputs stem from a single malicious blockchain spam incident that occurred back in 2011. In Ethereum, there is a storage fee applied on SSTORE to charge for adding items to the state, and the floating block limit system guarantees that even a malicious miner holds no substantial advantage in this aspect, but there is no system of a fee being imposed over time. Therefore, there are neither protections nor incentives against a Litecoin-like attack impacting the Ethereum blockchain as well. But what if such a mechanism existed? What if the blockchain could impose a rental fee?
The fundamental concept behind implementing a rental charge is straightforward. Each account would monitor how much space it occupies, incorporating the [ nonce, balance, code, state_root ] header RLP and the storage tree. Then, with every block, the balance would decrease by RENTFEE multiplied by the space utilized (which can be measured in bytes, with a simplicity normalization of each storage slot’s total memory load set to 64 bytes). If any account’s balance falls below zero, it would vanish from the blockchain. The challenging aspect lies in the implementation. Actually executing this model is easier in some respects and more complex in others than anticipated. The straightforward part is that there’s no need to update every account every block; you merely track the last block in which the account was altered and the space consumed by the account in the header RLP, then read the account each time computation accesses it. However, the difficult element is the removal of accounts with negative balances. One might assume that periodic scanning through all accounts to delete those with negative balances from the database would suffice; however, this approach does not fit well with Patricia trees. Consider a scenario where a new user joins the network at block 100000, wishes to download the state tree, and certain accounts have been deleted. Some nodes will need to retain the deleted accounts to account for the gaps, the hashes corresponding to nothing, in the trie. What if a light client requires proof of execution for a certain transaction? Then the node providing the proof must also include the deleted accounts. One potential solution is to have a “cleansing block” every 100000 blocks that reviews the entire state and purges the extraneous parts. Nevertheless, could there be a more refined solution?
Treaps
An elegant data structure in computer science is often referred to as a treap. A treap, as one might recognize or may not from the name, is a structure that serves as both a tree and a heap. To summarize the pertinent data structure theory, a heap is a binary tree where each node, except for the leaves, has one or two children, where every node has a lower value than its children, and the node with the lowest value is positioned at the top. What data structure theorists generally refer to as a tree is a binary tree in which values are organized in ascending order from left to right (i.e., a node is always greater than its left child and smaller than its right child, if present). A treap merges the two by having nodes containing both a key and a priority; the keys are arranged horizontally, while the priorities are aligned vertically. Although numerous heaps can exist for each set of priorities and numerous binary trees can be made for each set of values, it can be proven that only one treap corresponds to each set of (priority, value) pairs.
Moreover, there exists a straightforward (i.e., log-time) algorithm for both inserting and removing a value from the treap, and the mathematical attribute that ensures only one treap for every set of (priority, value) pairs means that treaps are deterministic. The combination of these characteristics makes treaps a promising candidate for substituting Patricia trees as the state tree data structure. However, this raises the question: what would we utilize for priorities? The response is clear: the priority of a node is determined by the anticipated block number at which the node would be removed. The cleaning procedure would simply involve continuously expelling nodes from the top of the treap, a log-time process that can be executed at the conclusion of each block.
Nonetheless, there exists an implementation challenge that complicates treaps for this purpose: treaps are not guaranteed to be shallow. For example, consider the values [[5, 100], [6, 120], [7, 140], [8, 160], [9, 180]]. Unfortunately, the treap for these values would appear as follows:
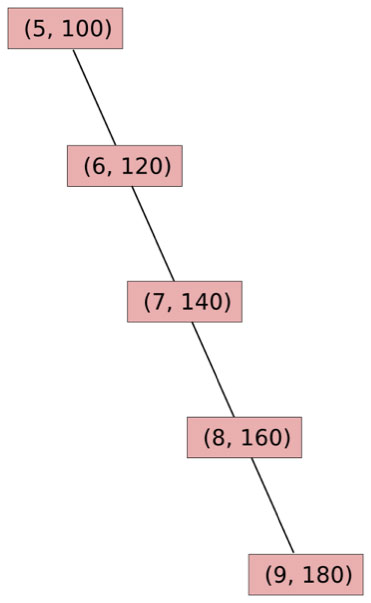
Now, envision that an attacker generates ten thousand addresses and arranges them in sorted order. The attacker subsequently creates an account with the first private key, providing it enough ether to endure until block 450000. The attacker then funds the second private key to last until block 450001, continues this process for the third private key until 450002, and so forth until the last account.susrvives until block 459999. All of these enter the blockchain. At this point, the blockchain will have a sequence of ten thousand values, each positioned below and to the right of all the preceding ones. Now, the assailant begins transmitting transactions to the addresses in the latter half of the list. Each of those transactions will necessitate ten thousand database interactions to pass through the treap for processing. Essentially, this constitutes a denial of service attack via trie manipulation. Can we lessen this risk by establishing priorities determined through a more sophisticated semi-randomized algorithm? Not really; even if priorities were utterly random, there exists a method through which the attacker could produce a 10000-length subsequence of accounts that maintain both address and priority in ascending order in a hundred million steps. Can we alleviate this by modifying the treap from the bottom up rather than from the top down? Again, no; the nature of these being Merkle trees means that we essentially must utilize functional algorithms to achieve any progress.
So what are our options? One potential strategy is to devise a way to counteract this attack. The most straightforward option might involve imposing a greater cost to acquiring priority the deeper you go in the tree. If the treap is presently 30 levels deep but your contribution would elevate it to 31 levels, the additional level would constitute an expense that must be covered. However, this necessitates that the trie nodes include a built-in height variable, complicating the data structure somewhat and making it less minimalist and pure. An alternative strategy is to leverage the concept behind treaps and create a data structure that achieves the same effect using traditional Patricia trees. This solution is employed in databases such as MySQL and is referred to as “indices“. Essentially, instead of having one trie, we utilize two. One trie maps addresses to account headers, while the other maps time-to-live to addresses. At the conclusion of each block, the left side of the TTL trie is scanned, and as long as nodes need to be deleted, they are consistently removed from both tries. When a new node is incorporated, it is added to both tries; similarly, when a node is updated, a naive implementation would modify it in both tries if the TTL changes as a result of the transaction. However, a more intricate setup could be established where the second update is performed only in a restricted subset of scenarios. For instance, one might implement a system where a node needs to “purchase TTL” in increments of 90 days, with this purchase occurring automatically each time a node is slated for removal – and if the node is financially incapacitated, it would naturally drop off the edge.
Consequences
Thus, we now possess three strategies: treaps with heights, tries with time-to-live indices, and the “cleansing block”. Which one proves most effective is an empirical inquiry; the TTL strategy may arguably integrate more easily into existing code, but any one of the three could turn out to be the most efficient, presuming the inefficiencies associated with implementing such a system alongside the usability issues of expiring contracts are outweighed by the benefits. What might the repercussions of any of these strategies be? Firstly, some contracts would need to start imposing a micro-fee; even passive units of code like an elliptic curve signature verifier would be required to continually expend resources to validate their existence, and those resources would have to be sourced. If a contract cannot sustain this, it could merely store a hash, placing the responsibility on the transaction sender to provide the contract with the code it is supposed to execute; the contract would subsequently verify the hash of the code, and if the hash is consistent, the code would be executed. Name-registry applications might opt to function somewhat differently, saving the majority of their registrations using a Merkle tree-based off-chain mechanism to mitigate their rent.
Nevertheless, there is also a more subtle implication: account nonce resets. For instance, suppose I own an account, and I engaged with some transactions from that account. To avert replay attacks (e.g., if I send 10 ETH to Bob, Bob should not be able to retransmit the same transaction to receive another 10 ETH), each transaction incorporates a “nonce” counter that increases after each transaction. Hence, the account header retains the current transaction nonce, and if the current nonce is 2, the only transaction that will be accepted is one with a nonce of 2, at which point the nonce will increment to 3. If accounts vanish, nonces could reset to 0, leading to potentially precarious situations if a user accumulates some funds in an account, then allows the balance to deplete to zero and the account to disappear, and then reapplies funds. One potential solution would involve setting a maximum block number for transactions, which could be designated to 10 days into the future by default, and then mandate all withdrawals to maintain sufficient balance for the account to function for another 10 days; this way, old transactions with nonce 0 would be too outdated to replay. However, this introduces an additional inefficiency that must be balanced against the benefits of blockchains imposing rent.
Furthermore, as an intriguing consideration, the history of the blockchain would regain importance; some dapps, wanting to preserve certain data indefinitely, would embed it within a transaction instead of the state, subsequently using prior block headers as an immutable rent-free datastore. The existence of such applications would necessitate that Ethereum clients maintain at least a headers-only version of the history, thus compromising Ethereum’s “the present state is all that matters” principle. Conversely, an alternative solution might involve utilizing a contract to maintain a Merkle mountain range, shifting the burden onto those users who benefit from specific pieces of information being secured to manage log-sized Merkle tree proofs while the contract remains under a kilobyte in size.
Lastly, what if the scarcity of storage space is not the most pressing point of pressure related to scalability? What if the principal issue lies with bandwidth or computation? If computation is the challenge, then several convenient tweaks could be implemented; for instance, the protocol might be extended to incorporate both transactions and state transition deltas into the block, allowing nodes the freedom to check only a portion of the deltas (say, 10%) and then swiftly communicate any inconsistencies among themselves. If bandwidth is the concern, then the issue becomes more complex, as it implies we cannot have every node downloading every transaction, thus necessitating some form of tree-chains solution to progress. Conversely, if space is indeed the issue, then rent-charging blockchains are very likely the appropriate path forward.

