“`html
One of the frustrations of the blockchain as a decentralized system is the considerable duration of delay before a transaction gets completed. A single confirmation in the Bitcoin network takes an average of ten minutes, but in practice, because of statistical phenomena, when one initiates a transaction, a confirmation can only be anticipated within ten minutes approximately 63.2% of the time; 36.8% of the time it will require more than ten minutes, 13.5% of the time longer than twenty minutes, and 0.25% of the time longer than an hour. Due to intricate technical aspects related to Finney attacks and sub-50% double spends, for numerous applications, even a single confirmation is inadequate; gambling platforms and exchanges frequently have to wait for three to six blocks to emerge, often exceeding an hour, before a deposit gets verified. In the period before a transaction is included in a block, security is nearly negligible; although many miners decline to propagate transactions that conflict with previously sent ones, there is no financial incentive for them to do so (in fact, quite the opposite), and some do not, making it possible to reverse an unconfirmed transaction with about a 10-20% success rate.
In numerous situations, this is acceptable; if you purchase a laptop online and manage to retract the funds five minutes later, the seller can simply cancel the shipment; online subscription services function in a similar manner. However, in the scenario of certain face-to-face transactions and virtual goods purchases, it is quite inconvenient. Specifically, in the context of Ethereum, the inconvenience is heightened; we aim to be not merely a currency, but a comprehensive platform for decentralized applications, and especially regarding non-financial applications, users typically expect a significantly quicker response time. Therefore, for our aims, having a blockchain that operates faster than 10 minutes is crucial. The inquiry then is, how low can we go, and if we decrease it too much, does that cause any destabilization?
Summary of Mining
To begin with, let’s provide a brief overview of how mining operates. The Bitcoin blockchain consists of a series of blocks, with each one linking to (i.e., containing the hash of) its predecessor. Each miner in the network endeavors to generate blocks by first gathering the required data (previous block, transactions, time, etc.), constructing the block header, and then repeatedly adjusting a value known as the nonce until the nonce fulfills a condition referred to as “proof of work” (or “mining algorithm”). This algorithm is stochastic and generally fails; on average, in Bitcoin, the network must collectively make approximately 1020 attempts before discovering a valid block. Once a random miner discovers a block that is valid (i.e., it references a legitimate prior block, its transactions and metadata are accurate, and its nonce meets the PoW condition), then that block is disseminated across the network and the process restarts. As compensation, the miner of that block receives a certain quantity of coins (25 BTC in Bitcoin) as a reward.
The “score” of a block is defined in a simplified manner as the total number of blocks in the chain leading back to the genesis (formally, it’s the cumulative mining difficulty, meaning that if the difficulty of the proof of work condition escalates, blocks generated under this new more rigorous condition count for more). The block with the highest score is regarded as “truth.” A subtle, yet significant, detail is that in this model, the motivation for miners is consistently to mine on the block with the highest score, because the block with the highest score is what users ultimately prioritize, and there are never any considerations that make a lower-score block preferable. If we alter the scoring model, then if we’re not vigilant this might change; but more on this later.
We can represent this kind of network as follows:
However, complications emerge when we consider that network propagation is not instantaneous. According to a 2013 study by Decker and Wattenhofer in Zurich, once a miner generates a block, on average it takes 6.5 seconds for the block to reach 50% of nodes, 40 seconds for it to reach 95% of nodes, with a mean delay of 12.6 seconds. Consequently, a more precise model might be:

This gives rise to the subsequent issue: if, at time T = 500, miner M mines a block B’ on top of B (where “on top of” indicates “pointing to as the previous block in the chain”), then miner N may not learn about the block until time T = 510, thus until T = 510 miner N will continue mining on B. If miner B produces a block in that timeframe, the rest of the network will reject miner B’s block because they have already observed miner M’s block which has an equivalent score:
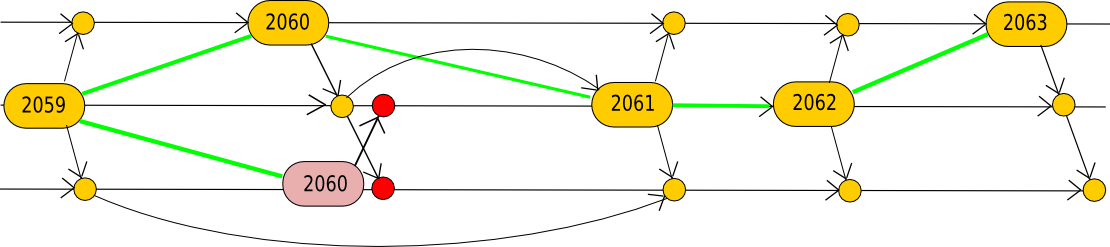
Stales, Efficiency, and Centralization
So what are the issues with this? In reality, there are two concerns. Firstly, it undermines the absolute strength of the network in defense against attacks. At a block time of 600 seconds, as in Bitcoin, this isn’t a problem; 12 seconds is quite a brief period, and Decker and Wattenhofer estimate the total stale rate to be around 1.7%. Therefore, an attacker does not necessarily require 50.001% of the network to execute a 51% assault; if the attacker is a single node, they would need only 0.983 / 1 + 0.983 = 49.5%. We can evaluate this through a mathematical expression: if transit time is 12 seconds, then after a block is produced, the network will generate stales for 12 seconds prior to the block propagating, so we can presume an average of 12 / 600 = 0.02 stales per valid block or a stale rate of 1.97%. However, with 60 seconds per block, we encounter 12 / 60 = 0.2 stales per valid block or a stale rate of 16.67%. At 12 seconds per block, we discover 12 / 12 = 1 stale per valid block, indicating a stale rate of 50%. Hence, we can observe the network becoming substantially weaker against attacks.
Nevertheless, there is also an additional unfavorable effect of stale rates. One of the more urgent challenges within the mining ecosystem is the issue of mining centralization. Presently, the majority of the Bitcoin network is divided into a small number of “mining pools”, centralized entities where miners collaborate resources to receive a more even reward, and the largest of these pools has been fluctuating between 33% and 51% of the network hash power for several months. In the future, even individual miners
“`may demonstrate hazardous; at present, 25% of all new bitcoin mining apparatus are emerging from a singular plant in Shenzhen, and if the unfavorable interpretation of my economic evaluation is accurate, it might ultimately transform into 25% of all Bitcoin miners being confined to one factory in Shenzhen.
How do stale rates influence centralization? The response is quite astute. Imagine having a network of 7000 pools each with 0.01% hashpower, alongside a single pool holding 30% hashpower. 70% of the time, the last block is generated by one of these miners, which the network acknowledges in 12 seconds, reflecting some inefficiency but ultimately maintaining fairness. However, 30% of the time, it is the mining pool with 30% hashpower that creates the last block; consequently, it “receives” the notification of the block immediately, resulting in a 0% stale rate, while all others continue to sustain their complete stale rate.
Due to the simplicity of our model, we can still engage in some calculations using an approximation in a closed form. With a transit time of 12 seconds and a block duration of 60 seconds, we ascertain a stale rate of 16.67% as elucidated earlier. The mining pool holding 30% will have a 0% stale rate for 30% of the time, resulting in an efficiency multiplier of 0.833 * 0.7 + 1 * 0.3 = 0.8831, while the rest will have an efficiency multiplier of 0.833; this translates to a 5.7% efficiency improvement, which is rather economically notable, especially for mining pools where the fee disparity is merely a fraction of a percent in either direction. Therefore, to achieve a 60-second block time, a more effective strategy is essential.
GHOST
The inception of a more effective method arises from a document titled “Fast Money Grows on Trees, not Chains“, published by Aviv Zohar and Yonatan Sompolinsky in December 2013. The concept posits that although stale blocks are not presently considered part of the total weight of the chain, they could be; hence they advocate for a blockchain scoring framework that incorporates stale blocks even if they are not part of the main chain. Consequently, even if the primary chain is only 50% effective or even 5% efficient, an assailant attempting a 51% attack would still need to surpass the weight of the complete network. This, in theory, addresses the efficiency dilemma down to 1-second block times. However, a challenge arises: the protocol, as delineated, only factors stales into the blockchain scoring; it does not allocate stales a block reward. Thus, it does nothing to rectify the centralization issue; indeed, with a 1-second block time, the most probable outcome would entail the 30% mining pool simply generating every block. Naturally, the 30% mining pool producing every block on the main chain is acceptable, but only if the blocks off chain are also equitably compensated, ensuring the 30% mining pool does not accumulate significantly more than 30% of the revenue. However, for that, rewarding stales will be necessary.
Currently, we can’t reward all stales perpetually; that would result in a bookkeeping catastrophe (the algorithm would need to meticulously verify that a newly included uncle had never been incorporated previously, thus necessitating an “uncle tree” alongside the transaction tree and state tree in each block) and, more critically, it would render double-spending costless. Therefore, let’s formulate our initial protocol, single-level GHOST, which executes the minimum requirement and accounts for uncles only up to one level (this is the methodology employed in Ethereum to date):
- Each block must reference a parent (i.e., the previous block) and may also include zero or more uncles. An “uncle” is defined as a block with a valid header (the block itself need not be legitimate, as we primarily care about its proof-of-work) which is a descendant of the grandparent block, but not the parent (i.e., the traditional lineage definition of “uncle” that you learned at age four).
- A block on the main chain receives a reward of 1. When a block encompasses an uncle, the uncle earns a reward of 7/8, and the block containing the uncle receives a reward of 1/16.
- The score of a block is nil for the genesis block; otherwise, it is the score of the parent added to the difficulty of the block multiplied by one plus the number of included uncles.
Thus, in the illustrated blockchain example provided earlier, we will have something resembling this:
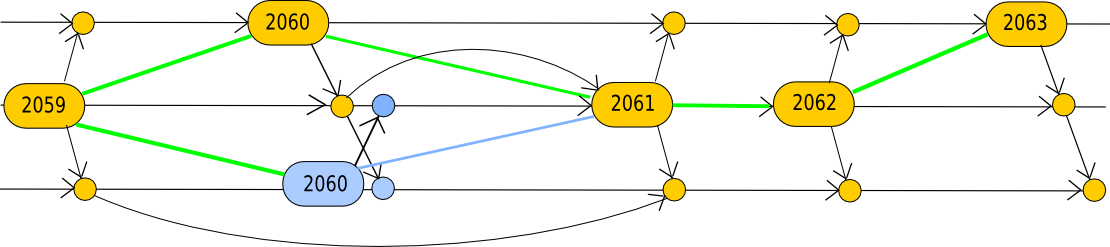
Here, the calculations become more intricate, prompting us to make some intuitive assertions and subsequently take a more relaxed approach by simulating the entire scenario. The fundamental intuitive assertion is this: in the basic mining protocol, for the reasons previously explained, the stale rate is approximately t/(T+t) where t signifies the transit time and T represents the block interval, as t/T of the time miners are mining on outdated information. With single-level GHOST, the failure threshold shifts from mining one stale to mining two stales in succession (as uncles can be included but relatives with a divergence of two or higher cannot), thus the stale rate should be (t/T)^2, approximately 2.7% instead of 16.7%. Now, let us utilize a Python script to verify that hypothesis:
### PRINTING RESULTS ### 1 1.0 10 10.2268527074 25 25.3904084273 5 ```html 4.93500893242 15 14.5675475882 Total blocks generated: 16687 Total blocks in chain: 16350 Effectiveness: 0.979804638341 Average uncles: 0.1584242596 Chain length: 14114 Block interval: 70.8516366728
The findings can be interpreted as such. The top five figures serve as a centralization metric; in this instance, it indicates that a miner with 25% hash power receives 25.39 times the reward of a miner with 1% hash power. The effectiveness is 0.9798, implying that 2.02% of all blocks are completely excluded, resulting in an average of 0.158 uncles per block; consequently, our assumptions regarding a ~16% stale ratio without uncle consideration and 2.7% with uncle consideration are nearly verified. It’s noteworthy that the actual block interval stands at 70.85 seconds because, despite a valid proof of work solution existing every 60 seconds, 2% of those are lost while 14% enter the subsequent block as an uncle instead of the primary chain.
At this point, an issue arises. The initial authors of the GHOST document omitted uncle/stale rewards, and although I think deviating from their guidance is warranted for the reasons outlined previously, they chose to forgo this for a specific rationale: it complicates the economic analysis. Specifically, when only the primary chain receives rewards, there exists a clear justification for consistently mining on the head rather than a previous block, primarily due to the fact that the sole differentiating factor between any two blocks is their score, with higher scores evidently being preferable to lower ones. However, once uncle rewards are introduced, additional factors complicate the scenario.
To illustrate, let’s consider when the main chain has its latest block M (score 502) with parent L (score 501) and further parent K (score 500). Assume also that K has two stale offsprings, both of which were created after M, thus there was no possibility for them to be included in M as uncles. By mining on M, you would generate a block with a score of 502 + 1 = 503 and a reward of 1. Conversely, by mining on L, you could incorporate K‘s children, yielding a block with a score of 501 + 1 + 2 = 504 and a reward of 1 + 0.0625 * 2 = 1.125.

Furthermore, there exists a selfish-mining-like assault against single-level GHOST. The premise is as such: if a mining pool possessing 25% hash power were to exclude any other blocks, in the short run, it would be detrimental to itself as it would miss out on the 1/16x nephew reward, but it would inflict greater harm upon others. Since mining is essentially a zero-sum endeavor over the long haul, as the block interval averages to maintain stable issuance, this suggests that the exclusion of uncles might, in fact, represent a dominant strategy, thus centralization worries are not entirely alleviated (specifically, they still persist 30% of the time). Moreover, if we pursue increasing the speed further, targeting a 12-second block time, the single-level model simply does not suffice. Here’s a result incorporating those metrics:
### DISPLAYING RESULTS ### 1 1.0 10 10.4567533177 15 16.3077390517 5 5.0859101624 25 29.6409432377 Total blocks generated: 83315 Total blocks in chain: 66866 Effectiveness: 0.802568565084 Average uncles: 0.491246459555 Chain length: 44839 Block interval: 22.3020138719
18% centralization
“`gain. Hence, we require a different approach.
A Fresh Approach
The initial concept I experimented with around a week prior was mandating that every block includes five uncles; this would, in a way, further decentralize the creation of each block, guaranteeing that no miner held a distinct edge in generating the next block. Given that the calculations for this are quite frustratingly complex (well, if you devote considerable time to it, perhaps you could devise something utilizing nested Poisson processes and combinatorial generating functions, but I’d prefer not to), here’s the simulation script. Take note that there are in fact two methods to implement the algorithm: require the parent to be the lowest-hash child of the grandparent, or mandate that the parent be the highest-score child of the grandparent. The initial method (to implement this independently, adjust line 56 to if newblock[“id”] > self.blocks[self.head][“id”]:, we obtain this:
### PRINTING RESULTS ### 1 1.0 10 9.59485744106 25 24.366668248 5 4.82484937616 15 14.0160823568 Total blocks produced: 8033 Total blocks in chain: 2312 Efficiency: 0.287812772314 Average uncles: 385.333333333 Length of chain: 6 Block time: 13333.3333333
Whoops! Let’s attempt the highest-score model instead:
### PRINTING RESULTS ### 1 1.0 10 9.76531271652 15 14.1038046954 5 5.00654546181 25 23.9234131003 Total blocks produced: 7989 Total blocks in chain: 6543 Efficiency: 0.819001126549 Average uncles: 9.06232686981 Length of chain: 722 Block time: 110.8033241
Here we observe a surprisingly counterintuitive outcome: the mining pool with 25% hash power yields merely 24 times the reward in comparison to a 1% hash power pool. Economic sublinearity remains a cryptoeconomic elusive goal, however, it also behaves somewhat like a perpetual motion machine; unless one depends on a specific resource that individuals possess a finite amount of (for instance, domestic heating demand, idle CPU capacity), there lacks a method to circumvent the reality that even if you devise some innovative sublinear arrangement, an entity with 25 times the input power can at minimum masquerade as 25 distinct entities and thereby claim a 1x reward. Consequently, we present clear (alright, fine, with 99 point something percent confidence) empirical evidence that the 25x miners are functioning suboptimally, indicating that the best approach in this context is not to consistently mine the block.with the utmost score.
The rationale here is the following: if you mine on a block that possesses the utmost score, then there exists a possibility that another entity might unearth a new uncle from one level back, subsequently mining a block atop that, thereby generating a new block at the same tier as your block but with a marginally superior score, leaving you in a disadvantaged position. However, if you attempt to be one of those uncles, the block with the highest score at the subsequent level will undoubtedly seek to include you, thus granting you the uncle reward. The emergence of one unorthodox strategy strongly implies the presence of additional, more exploitative, unconventional strategies, hence we will not pursue this path. Nevertheless, I opted to incorporate it into the blog entry to illustrate an instance of the inherent dangers.
So what is the optimal path ahead? It turns out that it is quite straightforward. Revert to single level GHOST, but permit uncles to originate from as far back as 5 blocks. Consequently, the child of a parent of a parent (hereinafter referred to as the -2,+1-ancestor) is a valid uncle, as is a -3,+1-ancestor, a -4,+1-ancestor, and a -5,+1-ancestor, while a -6,+1-ancestor or a -4,+2-ancestor (for example, c(c(P(P(P(P(P(head)))))) where no simplification is feasible) is not. Additionally, we enhance the uncle reward to 15/16 and reduce the nephew reward to 1/32. First, let’s ensure that it operates correctly under conventional strategies. In the GHOST simulation script, set UNCLE_DEPTH to 4, POW_SOLUTION_TIME to 12, TRANSIT_TIME to 12, UNCLE_REWARD_COEFF to 15/16 and NEPHEW_REWARD_COEFF to 1/32 and observe the results:
### PRINTING RESULTS ### 1 1.0 10 10.1329810896 25 25.6107014231 5 4.96386947539 15 15.0251826297 Total blocks created: 83426 Total blocks in chain: 77306 Efficiency: 0.926641574569 Average uncles: 0.693116362601 Length of chain: 45659 Block duration: 21.901487111
Entirely reasonable all around, although it should be noted that the actual block duration is 21 seconds due to inefficiency and uncles rather than the target of 12 seconds we aimed for. Now, let’s perform a few more experiments for enlightenment and amusement:
- UNCLE_REWARD_COEFF = 0.998, NEPHEW_REWARD_COEFF = 0.001 resulted in the 25% mining pool attaining approximately a 25.3x return, while establishing UNCLE_REWARD_COEFF = 7/8 and NEPHEW_REWARD_COEFF = 1/16 yields the 25% mining pool a 26.26% return. Clearly, setting the UNCLE_REWARD_COEFF to zero would entirely eliminate the benefit, thus it is beneficial to maintain it as close to one as feasible, but if it approaches one too closely, there will be no motivation to include uncles. UNCLE_REWARD_COEFF = 15/16 appears to be a reasonable compromise, allowing the 25% miner a 2.5% centralization advantage.
- Permitting uncles to reach back 50 blocks surprisingly results in minimal substantive efficiency improvements. The rationale is that the primary weakness of -5,+1 GHOST is its +1, rather than the -5; thus, stale c(c(P(P(..P(head)..)))) blocks pose the issue. In terms of centralization, with 0.998/0.001 rewards, this reduces the 25% mining pool’s reward essentially to 25.0x. With rewards of 15/16 and 1/32, there is no significant advantage compared to the -4,+1 approach.
- Allowing -4,+3 descendants enhances efficiency to effectively 100%, while bringing centralization nearly to zero, assuming 0.998/0.001 rewards, and provides negligible advantage when assuming 15/16 and 1/32 rewards.
- If we decrease the target block time to 3 seconds, efficiency falls to 66%, and the 25% miner receives a 31.5x return (that is a 26% centralization increase). If this is coupled with a -50,+1 condition, the effect remains negligible (25% -> 31.3x), but applying a -4,+3 rule increases efficiency to 83%, and the 25% miner achieves only a 27.5x return (the way to implement this in the simulation script is by adding after line 65 for c2 in self.children.get(c, {}): u[c2] = True for a -n,+2 condition, and then similarly nest down one more level for -n,+3). Additionally, the actual block time in all three of these scenarios hovers around 10 seconds.
- If we lower the target block time to 6 seconds, we observe an actual block duration of 15 seconds, with efficiency recorded at 82%, and the 25% miner achieving 26.8x even without any enhancements.
Now, let’s examine the other two dangers associated with limited GHOST that we previously mentioned: the non-head dominant strategy and the selfish-mining assault. It is important to note that there are indeed two non-head strategies: attempting to acquire more uncles,and strive to act as an uncle. Attempting to incorporate more uncles proved advantageous in the -2,+1 scenario, and endeavoring to act as an uncle was beneficial in the circumstance of my unsuccessful mandatory-5-uncles concept. Trying to be an uncle isn’t particularly beneficial when not many uncles are necessary, since the reason that alternative approach worked in the mandatory-5-uncle situation is due to a new block being ineffective for continued mining without siblings. Therefore, the only potentially troublesome strategy is attempting to add uncles. In the single-block instance, it was an issue, but here it isn’t, because the majority of uncles that can be added after n blocks can also be appended after n+1 blocks, so the practical impact of this will be minimal.
The selfish-mining assault also ceases to function for a comparable rationale. If you neglect to include uncles, the individual following you will. There are four opportunities for an uncle to be accepted, thus not including uncles turns into a 4-player prisoner’s dilemma among unidentified participants – a game that is fated to conclude unfavorably for all involved (except, of course, the uncles themselves). Additionally, there is one final issue with this strategy: we observed that recompensing all uncles renders 51% attacks devoid of cost, so are they devoid of cost here? Beyond a single block, the response is no; while the first block of a fork attempt will be accepted as an uncle and obtain its 15/16x reward, the second, third, and all subsequent ones will not, thus beginning from two confirmations, attacks still impose nearly the same costs on miners as they did previously.
Twelve seconds, honestly?
The most unexpected revelation regarding Decker and Wattenhofer’s findings is the astonishing amount of time it takes for blocks to propagate – an incredibly sluggish 12 seconds. In Decker and Wattenhofer’s evaluation, the 12-second interval is primarily due to the necessity to download and verify the blocks themselves; in other words, the procedure that Bitcoin clients adhere to is:
def on_receive_block(b): if not verify_pow_and_header(b): return if not verify_transactions(b): return accept(b) start_broadcasting(b)
Nevertheless, Decker and Wattenhofer did recommend a more effective strategy that resembles the following:
def on_receive_header(h): if not verify_pow_and_header(h): return ask_for_full_block(h, callback) start_broadcasting(h) def callback(b): start_broadcasting(b) if not verify_transactions(b): stop_broadcasting(b) return accept(b)
This permits all procedures to occur concurrently; headers can be broadcast initially, followed by blocks, and the verifications do not need to be executed sequentially. Although Decker and Wattenhofer do not offer their personal assessment, intuitively it appears that this could enhance propagation speed by 25-50%. The algorithm remains unexploitable because to generate an invalid block that clears the first verification, a miner would still need to create a valid proof of work, so there is nothing a miner could profit from. Another observation made in the paper is that the transmission time, past a certain threshold, scales with block size; hence, reducing block size by 50% will likely diminish transmission time to around 25-40%; the portion of transmission time that doesn’t scale is roughly 2 seconds. Thus, a target block time of 3 seconds (and an actual block time of 5 seconds) may indeed be quite feasible. As always, we will proceed cautiously at the outset and not push boundaries too far, but achieving a block time of 12 seconds does seem highly attainable.

