Proof of stake remains one of the most debated topics in the cryptocurrency arena. While the concept has several undeniable advantages, including increased efficiency, a broader security margin, and enhanced resistance to hardware centralization issues, proof of stake mechanisms are often significantly more intricate than their proof of work counterparts. There exists considerable doubt regarding the viability of proof of stake, especially concerning the purportedly central “nothing at stake” dilemma. Nevertheless, these challenges are addressable, and a solid case can be made that proof of stake, along with its advantages, can be effectively implemented—albeit at a sensible cost. This article aims to clarify what this cost entails and how its effects can be mitigated.
Economic Sets and Nothing at Stake
To begin, let’s frame the discussion. The intent of a consensus algorithm is essentially to enable secure updates of a state in accordance with specific state transition regulations, where the authority to execute these transitions is shared among an economic set. An economic set is a grouping of participants authorized to collaboratively carry out transitions through a particular algorithm. A vital characteristic that must be maintained by the economic set for consensus to function effectively is its requirement to be securely decentralized—indicating that no individual or colluding group can dominate the majority of the set, even if they possess a substantial quantity of capital and financial motivation. To date, we are aware of three securely decentralized economic sets, with each corresponding to a consensus algorithm:
- Computational power owners: conventional proof of work, or TaPoW. It is important to note that this exists in specialized hardware, and (ideally) in general-purpose hardware variations.
- Stakeholders: a multitude of variations of proof of stake
- A user’s social network: Consensus akin to Ripple/Stellar styles
It’s worth mentioning that there have been recent endeavors to create consensus algorithms grounded in traditional Byzantine fault tolerance theory. However, all these methodologies are founded on an M-of-N security framework, and the notion of “Byzantine fault tolerance” alone does not clarify which set the N should be sampled from. In most instances, stakeholders are utilized, so we’ll regard such neo-BFT frameworks merely as clever subcategories of “proof of stake”.
Proof of work has an advantageous attribute that facilitates the design of effective algorithms: involvement in the economic set necessitates the utilization of a resource external to the system. This means that when a miner contributes to the blockchain, they must decide which among various forks to support (or if they should attempt to initiate a new fork), and these choices are mutually exclusive. Double-voting, including cases where a subsequent vote is cast years after the initial one, is unbeneficial as it necessitates splitting one’s mining power across multiple votes; the optimal strategy is consistently to concentrate your mining power on the fork you believe has the highest likelihood of succeeding.
Conversely, with proof of stake, the dynamics change. While entry into the economic set may be burdensome (though, as we shall see, this is not universally the case), voting incurs no cost. Consequently, “naive proof of stake” mechanisms, which attempt to replicate proof of work by transforming each coin into a “simulated mining rig” with a certain probability per second of making the related account available for block signing, possess a crucial vulnerability: when multiple forks arise, the ideal strategy is to cast votes on all forks simultaneously. This lies at the heart of the “nothing at stake” issue.

There exists an argument suggesting it might be illogical for a user to support only one fork in a proof-of-stake context: “altruism-prime.” Altruism-prime is essentially a blend of genuine altruism (by users or software architects), manifested both as a direct concern for the well-being of others and the network, as well as a psychological moral restraint against undertaking actions deemed clearly malevolent (like double-voting), along with the “fake altruism” that arises because coin holders wish to prevent the value of their assets from declining.
Unfortunately, altruism-prime cannot be depended upon solely, as the value of coins stemming from protocol integrity is a public good and therefore will be underprovided (for instance, if there are 1000 stakeholders, and each of their actions has merely a 1% chance of being “pivotal” in leading to a successful assault that could diminish coin value to zero, then each participant would accept a bribe equivalent to only 1% of their holdings). In a distribution comparable to the Ethereum genesis block, depending on how one assesses the probability of each user being pivotal, the necessary sum of bribes would range between 0.3% to 8.6% of the overall stake (or potentially less if an attack isn’t fatal to the currency). Nevertheless, altruism-prime remains an essential concept that algorithm developers should consider to maximize its benefits, should it function effectively.
Short and Long Range
When we concentrate specifically on short-range forks—which last for fewer than a specified number of blocks, perhaps 3000—there actually exists a resolution to the nothing at stake dilemma: security deposits. To qualify for rewards by voting on a block, a user must place a security deposit, and if they are discovered voting on several forks, then proof of that action can be inserted into the primary chain, stripping away the reward. Thus, supporting only one fork once more becomes the preferred strategy.

Another category of strategies, referred to as “Slasher 2.0” (as opposed to Slasher 1.0, the original security deposit-centric proof of stake mechanism), involves merely penalizing participants who vote on the incorrect fork, rather than those who double-vote. This rendersanalysis considerably more straightforward, as it eliminates the requirement to pre-identify voters many blocks ahead to thwart probabilistic double-voting tactics, although it does incur the drawback that individuals may hesitate to endorse anything if there are two options for a block at a certain height. If we wish to provide users the ability to sign in such scenarios, a variation of logarithmic scoring rules can be applied (refer to here for a more in-depth examination). For the scope of this discussion, Slasher 1.0 and Slasher 2.0 possess identical characteristics.

The rationale for why this only applies to short-range forks is quite clear: the user must eventually have the authority to retrieve the security deposit, and upon withdrawal of the deposit, there is no longer any motivation to refrain from voting on a long-range fork originating far back in time utilizing those assets. One category of strategies that seeks to address this is by making the deposit permanent, yet these methods have their own challenges: unless a coin’s value consistently appreciates to continuously accommodate new signers, the consensus set risks becoming established as a type of perpetual nobility. Considering that a significant ideological grievance that has propelled cryptocurrency’s appeal is precisely the tendency for centralization to solidify into nobilities that maintain enduring power, replicating such a feature would likely be seen as intolerable by most participants, at least for blockchains intended to be everlasting. A nobility structure might indeed be the apt approach for specialized temporary blockchains designed to perish quickly (e.g., one might envision such a blockchain existing for a session of a blockchain-based game).
One category of solutions to this challenge is to merge the Slasher mechanism outlined above for short-range forks with a backup, transactions-as-proof-of-stake, for long-range forks. TaPoS fundamentally functions by incorporating transaction fees as a component of a block’s “score” (and mandating each transaction to include some bytes from a recent block hash to prevent trivial transferability), with the premise being that a successful attack fork must allocate a substantial amount of fees to catch up. However, this hybrid methodology contains a fundamental weakness: if we posit that the chance of an attack succeeding is nearly negligible, then every signer has an incentive to provide a service of re-signing all of their transactions onto a new blockchain in exchange for a minor fee; thus, a zero probability of attacks succeeding is not game-theoretically robust. Does it sound far-fetched that every user sets up their own node.js web application to accept bribes? If so, there’s a much simpler alternative: sell old, unused private keys on the black market. Even absent black markets, a proof-of-stake system would perpetually face risks from individuals who initially participated in the pre-sale and held a share of genesis block issuance eventually reuniting to initiate a fork.
In light of all the aforementioned arguments, we can confidently conclude that the risk of an attacker constructing a fork from arbitrarily long range is, regrettably, a fundamental issue, and in all non-degenerate implementations, the problem is catastrophic for a proof-of-stake algorithm’s success within the proof-of-work security framework. Nevertheless, we can navigate this inherent obstacle with a minor, yet fundamentally important, revision in the security model.
Weak Subjectivity
While numerous methods categorize consensus algorithms, the distinction we will emphasize for the remainder of this discussion is as follows. Firstly, we will present the two most prevalent paradigms today:
- Objective: a new node joining the network with no prior knowledge except (i) the protocol description and (ii) the array of all blocks and other “crucial” messages released can autonomously reach the identical conclusion as the rest of the network regarding the current state.
- Subjective: the system comprises stable states where various nodes arrive at different conclusions, necessitating a considerable amount of social information (i.e., reputation) to participate.
Systems utilizing social networks as their consensus set (e.g., Ripple) are intrinsically subjective; a new node with no knowledge beyond the protocol and the data can be persuaded by an adversary that their 100000 nodes are reliable, and in the absence of reputation, there is no mechanism to counteract that assault. Proof of work, by contrast, is objective: the current state is always the one that embodies the highest anticipated amount of proof of work.
Now, for proof of stake, we will introduce a third paradigm:
- Weakly subjective: a new node entering the network with no knowledge beyond (i) the protocol definition, (ii) the collection of all blocks and other “critical” messages published, and (iii) a state from less than N blocks ago that is confirmed to be valid can independently attain the same conclusion as the rest of the network regarding the current state, unless there exists an attacker that consistently holds more than X percent control over the consensus set.
Within this framework, we can clearly observe how proof of stake functions effectively: we simply prohibit nodes from reverting more than N blocks, setting N to the security deposit duration. In other words, if state S has been verified and has become an ancestor of at least N valid states, then thereafter no state S’ that isn’t a descendant of S can be deemed valid. Long-range attacks are no longer of concern, for the simple reason that we have explicitly declared that long-range forks are invalid as part of the protocol framework. This rule is evidently weakly subjective, with the additional benefit that X = 100% (i.e., no attack can induce permanent disruption unless it persists beyond N blocks).
Another weakly subjective scoring approach is exponential subjective scoring, defined as follows:
- Each state S carries a “score” and a “gravity”
- score(genesis) = 0, gravity(genesis) = 1
- score(block) = score(block.parent) + weight(block) * gravity(block.parent), wherein weight(block) is typically 1, although more sophisticated weight functions may also be deployed (e.g., in Bitcoin, weight(block) = block.difficulty can be quite effective)
- If a node encounters a new block B’ with B as progenitor, then if n is the size of the longest lineage of descendants originating from B at that moment, gravity(B’) = gravity(B) * 0.99 ^ n (note that values other than 0.99 are also applicable).

In essence, we explicitly sanction forks that emerge later. ESS possesses the characteristic that, in contrast to simpler methods based on subjectivity, it largely prevents enduring network divides; if the duration between the initial node in the network learning about block B and the final node in the network learning about block B spans an interval of k blocks, then a fork becomes untenable unless the lengths of the two forks remain perpetually within approximately k percent of one another (in such a case, the differing gravities of the forks will assure that half of the network will consistently view one fork as superior while the other half will back the alternative fork). Thus, ESS is weakly subjective with X roughly indicative of how near to a 50/50 network division the attacker can engineer (for example, if the assailant can fabricate a 70/30 split, then X = 0.29).
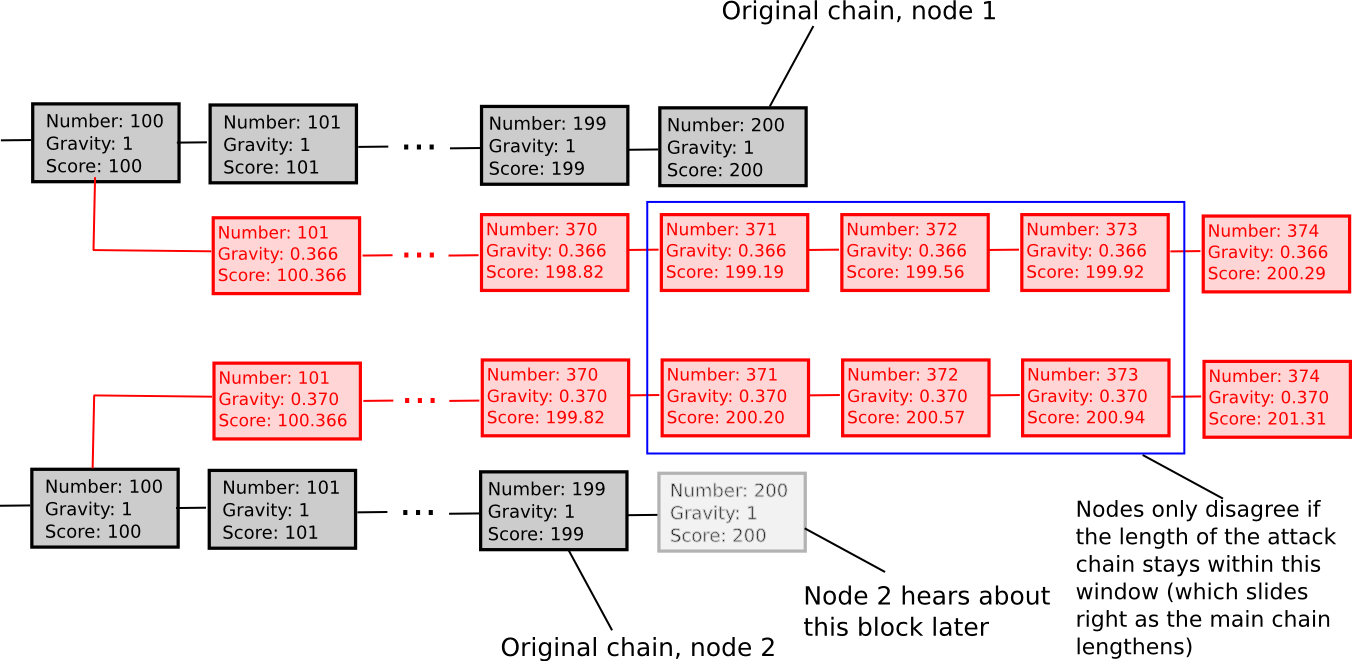
Overall, the “max revert N blocks” guideline is preferable and less complicated, yet ESS might demonstrate more viability in circumstances where users are comfortable with significant levels of subjectivity (i.e., N being minimal) in exchange for a swift progression to exceptionally high security levels (i.e., resistant to a 99% attack after N blocks).
Consequences
What might a world driven by weakly subjective consensus resemble? Primarily, nodes that are consistently online will be secure; in such scenarios, weak subjectivity is, by definition, equivalent to objectivity. Nodes that occasionally go online, or at least once every N blocks, will also be secure, as they will be able to continuously obtain an updated status of the network. However, new nodes entering the network, and nodes that reappear online after a protracted absence, might not have the consensus mechanism reliably safeguarding them. Fortunately, the remedy is straightforward: the first time they register, and each time they remain offline for an exceedingly long period, they only need to acquire a recent block hash from a friend, a blockchain explorer, or merely their software provider, and input it into their blockchain client as a “checkpoint.” They will then be capable of securely updating their perception of the present status from that point onward.
This security premise, the concept of “acquiring a block hash from a friend,” may appear tenuous to many; Bitcoin developers frequently argue that if the solution to long-range attacks hinges on some alternative deciding mechanism X, then the security of the blockchain ultimately rests upon X, and thus the algorithm is essentially no more secure than using X directly – suggesting that most X, including our social-consensus-driven method, are insecure.
However, this reasoning overlooks why consensus algorithms exist in the first place. Consensus is inherently a social process, and humans are quite adept at reaching consensus independently without any assistance from algorithms; perhaps the most poignant example is the Rai stones, where a tribe in Yap effectively maintained a blockchain documenting changes to the ownership of stones (utilized as a Bitcoin-like zero-intrinsic-value asset) as part of its collective memory. The reason why consensus algorithms are necessary is, quite simply, due to the fact that humans lack infinite computational capacity, and tend to rely on software agents to uphold consensus for us. Software agents are exceptionally intelligent, as they can uphold consensus over extremely large states with exceedingly intricate rulesets with flawless accuracy, but they are also quite oblivious, in that they possess very limited social information; the challenge for consensus algorithms is to develop a mechanism that demands as minimal social information input as possible.
Weak subjectivity is precisely the optimal solution. It addresses the long-range issues associated with proof of stake by drawing upon human-driven social insights, yet it entrusts a consensus algorithm with the function of accelerating consensus from multiple weeks to twelve seconds and permitting the implementation of highly intricate rulesets across a vast state. The responsibility of human-driven consensus is relegated to maintaining agreement on block hashes over extended periods, a task at which people excel. A hypothetical oppressive regime that possesses sufficient power to create uncertainty regarding the authentic value of a block hash from a year prior would also have enough strength to override any proof of work algorithm or instigate confusion regarding the blockchain protocol’s regulations.
Note that we do not need to set N; theoretically, we could devise an algorithm that enables users to keep their deposits secured for durations exceeding N blocks, allowing users to leverage those deposits for a much more nuanced evaluation of their security level. For instance, if a user has not logged in since T blocks ago, and 23% of deposits have a term length greater than T, the user can formulate their subjective scoring criterion that disregards signatures with more recent deposits, thereby fortifying their security against assaults involving up to 11.5% of the total stake. An ascending interest rate curve may be utilized to motivate longer-term deposits over shorter ones, or for simplicity, we may just depend on altruism-prime.
Marginal Cost: The Other Objection
One criticism of long-term deposits is that they encourage users to keep their funds immobilized, which is inefficient, presenting the identical issue as proof of work. Nonetheless, there are four rebuttals to this.
Firstly, marginal cost does not equate to total cost, and the ratio of total cost divided by marginal cost is substantially lower for proof of stake compared to proof of work. A user will likely experience nearly no discomfort from securing 50% of their capital for several months, a minimal amount of distress from securing 70%, but would find securing over 85% unbearable without a significant incentive. Moreover, distinct users have varying preferences for how willing they are to immobilize capital. Together, these two factors suggest that regardless of what the equilibrium interest rate ultimately is, the overwhelming majority of capital will be locked at levels significantly beneath marginal cost.
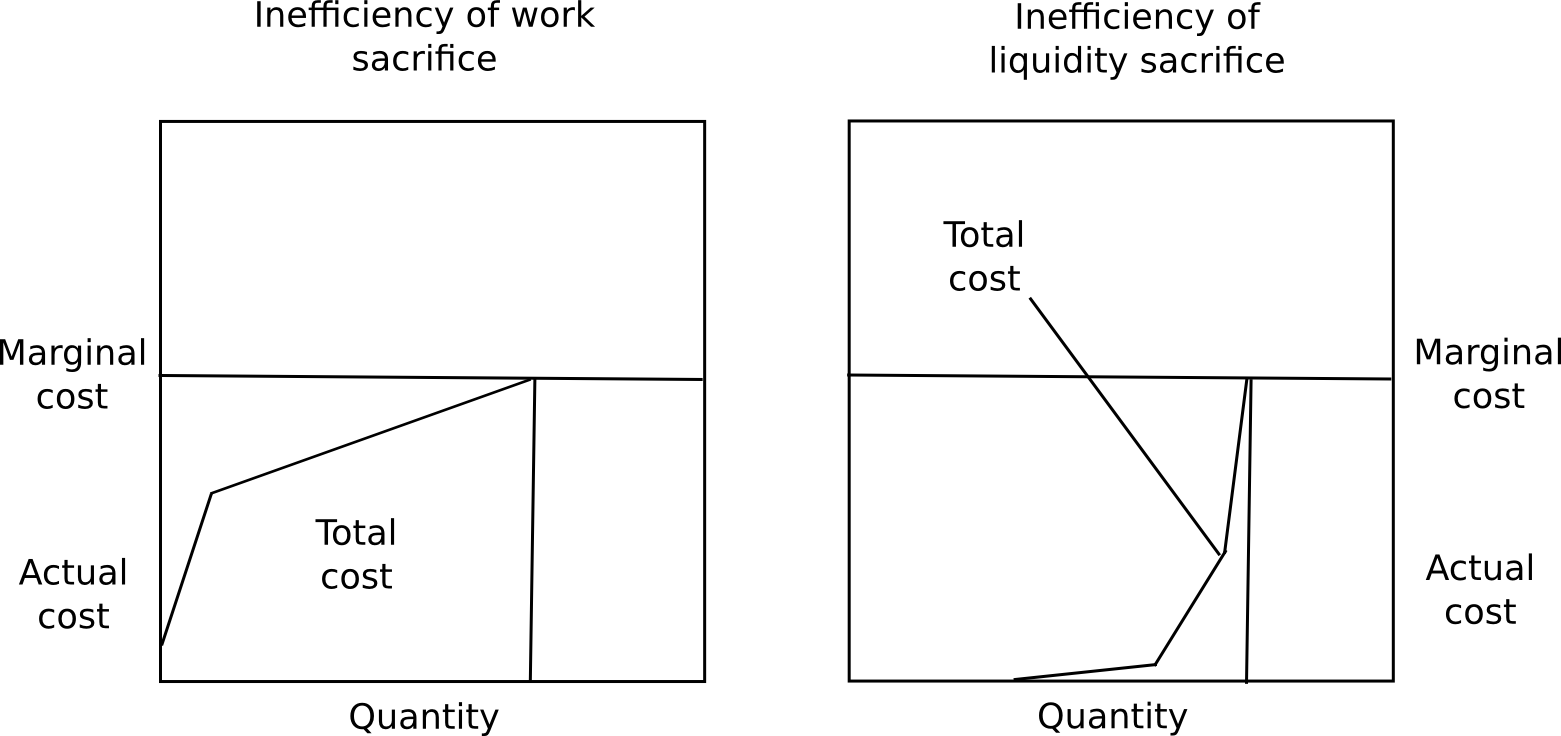
Secondly, immobilizing funds constitutes a private expense, yet also serves as a public benefit. The occurrence of immobilized funds signifies that there is a diminished money supply accessible for transactional activities, consequently driving up the value of the currency, thereby reallocating resources to others and generating a societal advantage. Thirdly, security deposits represent an extremely reliable store of value, hence (i) they replace the function of cash as a personal crisis safeguarding mechanism, and (ii) numerous users can secure loans in the same currency backed by the security deposit. Ultimately, since proof of stake can indeed revoke deposits for misconduct, rather than merely dispensing rewards, it can achieve a level of security considerably exceeding that of rewards, whereas in the case of proof of work, the level of security can merely match the level of rewards. There exists no means for a proof of work protocol to annihilate the ASICs of errant miners.
Fortunately, there exists a methodology to verify those theories: initiate a proof of stake currency with a staking reward of 1%, 2%, 3%, etc per annum, and observe the proportion of coins that convert to deposits in each scenario. Participants will not act contrary to their interests, thus we can merely gauge the amount of funds expended on consensus as an indicator of the inefficiency introduced by the consensus algorithm; if proof of stake maintains a reasonable security level at a substantially lower reward level than proof of work, then we can ascertain that proof of stake is a more efficient consensus mechanism, using the participation levels at varying reward rates to accurately gauge the relationship between total expense and marginal cost. Ultimately, it may require several years to precisely comprehend the magnitude of the costs associated with capital lockup.
In summary, we now confidently recognize that (i) proof of stake algorithms can be secured effectively, and weak subjectivity is both essential and adequate as a crucial revision in the security framework to navigate around nothing-at-stake apprehensions to achieve this aim, and (ii) there are significant economic grounds to assert that proof of stake is considerably more economically efficient than proof of work. Proof of stake is not a mystery; the recent six months of formal development and research have clarified the precise strengths and vulnerabilities, at least to the same degree as in proof of work, where uncertainties regarding mining centralization may persist indefinitely. Now, it is simply a matter of standardizing the algorithms and providing blockchain developers the liberty to choose.

