The cryptocurrency 2.0 sector has made significant advancements over the past year in enhancing blockchain technology, including the establishment and, in certain instances, the actual implementation of proof of stake models such as Slasher and DPOS, various types of scalable blockchain mechanisms, blockchains utilizing “leaderless consensus” strategies derived from traditional Byzantine fault tolerance principles, along with economic components like Schelling consensus frameworks and stable currencies. Each of these technologies addresses critical shortcomings of the blockchain model in comparison to centralized servers: scalability minimizes size limitations and transaction expenses, leaderless consensus mitigates various types of vulnerabilities, enhanced PoS consensus frameworks lower consensus expenses and bolster security, and Schelling consensus enables blockchains to be “cognizant” of real-world information. Nevertheless, there remains one aspect of the equation that all methodologies thus far have not yet resolved: privacy.
Currency, Dapps and Privacy
Bitcoin offers its users a rather distinctive array of trade-offs concerning financial confidentiality. While Bitcoin performs significantly better than any previous system at safeguarding the actual identities associated with each of its accounts – superior to fiat and banking systems due to the absence of identity registration, and better than cash as it can be used in conjunction with Tor to fully obscure physical location, the existence of the Bitcoin blockchain implies that the genuine transactions executed by the accounts are more visible than ever – neither the US government, nor China, nor the thirteen-year-old hacker down the block require even a warrant to ascertain precisely which account transferred how much BTC to which recipient at what specific moment. In general, these two opposing forces pull Bitcoin in conflicting directions, and it is not entirely apparent which one predominates.
In regard to Ethereum, the scenario is theoretically similar, but in practice, it differs considerably. Bitcoin is a blockchain designed for currency, and currency is, by its nature, a highly fungible entity. There are methods like merge avoidance that enable users to effectively masquerade as 100 distinct accounts, with their wallet managing the separation behind the scenes. Coinjoin can be implemented to “shuffle” assets in a decentralized manner, and centralized mixers are also a viable option, particularly when combining several of them. Ethereum, on the contrary, is meant to store the interim state of any type of processes or relationships, and regrettably, it is often the case that many processes or connections that are significantly more intricate than money are intrinsically “account-based”, which results in considerable costs when attempting to obscure one’s actions through multiple accounts. Therefore, Ethereum, in its current form, often embodies the transparency aspect of blockchain technology far more than the privacy aspect (although those keen on using Ethereum for currency can certainly construct higher-privacy cash protocols within subcurrencies).
Now, the inquiry arises, what happens when individuals genuinely desire privacy, yet a Diaspora-style self-hosting solution or a Zerocash-style zero-knowledge-proof approach is, for any reason, unfeasible – for instance, if we wish to carry out computations that necessitate aggregating multiple users’ private data? Even if we resolve scalability and blockchain data assets, will the absence of privacy inherently linked to blockchains mean that we simply have to revert to relying on centralized servers? Or can we devise a protocol that merges the advantages of both realms: a blockchain-like system that provides decentralized authority not only over the permission to modify the state but also over the entitlement to access the information entirely?
Interestingly, such a system exists within the realm of possibility, and was even postulated by Nick Szabo in 1998 under the label of “God protocols” (although, as Nick Szabo has noted, we should avoid using that term for the protocols we are about to outline here since God is generally considered or even defined to be Pareto-superior to everything else and as we will soon demonstrate, these protocols are quite distant from that); but now with the emergence of Bitcoin-style cryptoeconomic technology, the creation of such a protocol may, for the first time, genuinely be practical. What is this protocol? To assign it a reasonably technically precise yet still comprehensible name, we will refer to it as a “secret sharing DAO”.
Fundamentals: Secret Sharing
To bypass the entertaining technical nuances and head directly to applications, click here
Secret computation networks depend on two core components to store data in a decentralized manner. The first is secret sharing. Secret sharing fundamentally enables data to be kept in a decentralized manner across N participants in such a way that any K participants can collaborate to reconstruct the information, but K-1 participants are unable to retrieveany details whatsoever. N and K may be adjusted to any preferred values; it merely requires a few minor parameter adjustments in the algorithm.
The most straightforward way to mathematically represent secret sharing is as follows. We understand that two points define a line:
Thus, to execute 2-of-N secret sharing, we take our secret S, produce a random slope m, and formulate the line y = mx + S. We then provide the N participants with the points on the line (1, m + S), (2, 2m + S), (3, 3m + S), etc. Any two of them can reconstruct the line and retrieve the original secret, while a single individual can accomplish nothing; if you obtain the point (4, 12), that could belong to the line y = 2x + 4, or y = -10x + 52, or y = 305445x – 1221768. To implement 3-of-N secret sharing, we simply create a parabola instead, and provide individuals points on the parabola:
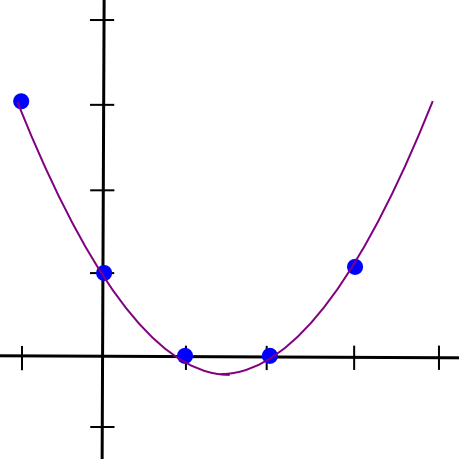
Parabolas possess the characteristic that any three points on a parabola can be utilized to reconstruct the parabola (and no one or two points are adequate), so fundamentally the same method is applicable. And, more broadly, to implement K-of-N secret sharing, we employ a polynomial of degree K-1 in a similar manner. There exists a collection of algorithms for retrieving the polynomial from a sufficient set of points in all such scenarios; they are elaborated on in our previous article on erasure coding.
This is how the secret sharing DAO will manage data. Rather than having each participating node in the consensus hold a copy of the entire system state, each participating node in the consensus will maintain a set of shares of the state – points on polynomials, one point on a different polynomial for each variable that constitutes part of the state.
Fundamentals: Computation
Now, how does the secret sharing DAO conduct computation? For this, we utilize a series of algorithms called secure multiparty computation (SMPC). The core principle behind SMPC is that there are methods to take data which is distributed among N parties using secret sharing, execute computations on it in a decentralized manner, and ultimately arrive at the result secret-shared among the parties, all without ever reconstructing any of the data on a single device.
SMPC with addition is straightforward. To illustrate how, let’s revisit the two-points-make-a-line example, but now let’s consider two lines:
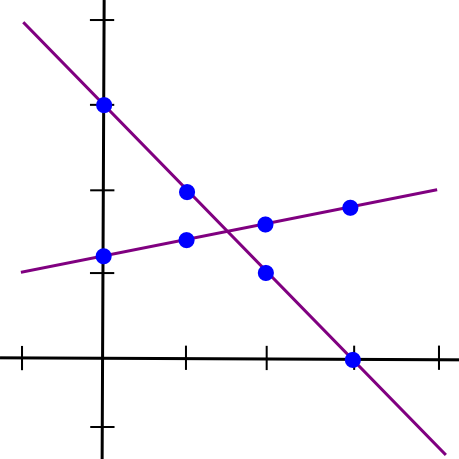
Assume that the x=1 point of both lines A and B is stored by device P[1], the x=2 point is saved by device P[2], and so forth. Now, suppose that P[1] calculates a new value, C(1) = A(1) + B(1), and B computes C(2) = A(2) + B(2). Now, let’s sketch a line through those two points:
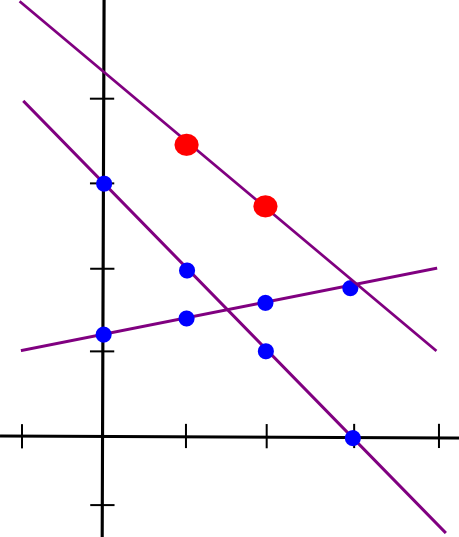
Thus, we obtain a new line, C, such that C = A + B at points x=1 and x=2. However, the intriguing aspect is that this new line is, in fact, equal to A + B at every point:
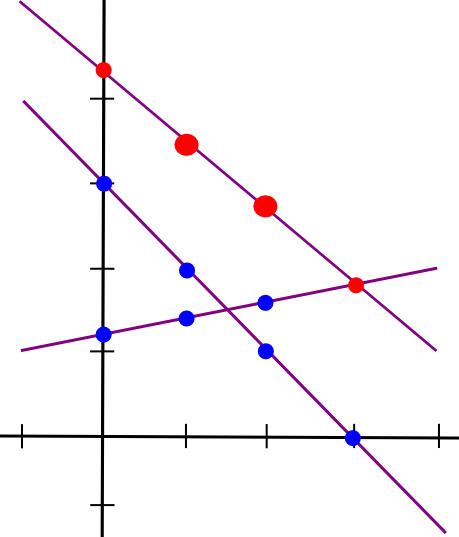
Therefore, we establish a rule: sums of secret shares (at the identical x coordinate) are secret shares of the overall sum. Utilizing this principle (which also extends to higher dimensions), we can transform secret shares of a and secret shares of b into secret shares of a+b, all without ever reconstructing a and b themselves. Multiplication by a known constant value operates in the same manner: k times the ith secret share of a is equivalent to the ith secret share of a*k.
Multiplication of two secret shared quantities, regrettably, is far more complex. The process will entail several steps to elucidate, and since it is fairly intricate in any case, it is advisable to conduct this for arbitrary polynomials right away. Here’s the intriguing part. First, let’s assume there are values a and b, secret shared among parties P[1] … P[n], where a[i] signifies the ith share of a (and similarly for b[i] and b). We commence like this:
Now, one approach that you might consider is, if we can simply create a new polynomial c = a + b by ensuring every participant tracks c[i] = a[i] + b[i], is it possible to apply the same principle to multiplication? The response is, surprisingly, affirmative, yet it comes with a substantial issue: the resultant polynomial has a degree that is double that of the initial ones. For instance, if the initial polynomials were y = x + 5 and y = 2x – 3, their multiplication would yield y = 2x^2 + 7x – 15. Therefore, if we perform multiplication repeatedly, the polynomial would grow too large for the N group to manage.
To mitigate this issue, we execute a type of rebasing protocol where we transform the shares of the larger polynomial into shares of a polynomial with the original degree. The functioning is as follows. Initially, party P[i] produces a new random polynomial, matching the degree of a and b, which evaluates to c[i] = a[i]*b[i] at zero and subsequently distributes points along that polynomial (i.e., shares of c[i]) to all participants.
Consequently, P[j] now possesses c[i][j] for every i. Given this information, P[j] computes c[j], ensuring that everyone holds secret shares of c, based on a polynomial that maintains the same degree as a and b.
To accomplish this, we utilized a clever technique of secret sharing: since the mathematics of secret sharing itself involves nothing but additions and multiplications with known constants, the two layers of secret sharing are commutative: if we first implement secret sharing layer A and then layer B, we can remove layer A prior to layer B and still maintain protection. This enables us to transition from a higher-degree polynomial to a lower-degree polynomial while concealing the intermediate values – instead, the intermediate phase involved both layers being applied simultaneously.
With operations of addition and multiplication over 0 and 1, we possess the capacity to execute arbitrary circuits within the SMPC framework. We can define:
- AND(a, b) = a * b
- OR(a, b) = a + b – a * b
- XOR(a, b) = a + b – 2 * a * b
- NOT(a) = 1 – a
Thus, we can conduct any programs desired, although with one significant limitation: secret conditional branching is not feasible. In other words, if we had a computation if (x == 5)
There are two solutions to this concern. Firstly, we can utilize multiplication as a “poor man’s if” – substitute an expression like if (x == 5)
The secret-sharing based protocol outlined above represents merely one approach to accomplishing relatively straightforward SMPC; alternative methods exist, and ensuring security also necessitates the addition of a verifiable secret sharing layer above, but that lies beyond the scope of this article – the preceding explanation aims simply to illustrate how a minimal implementation is feasible.
Creating a Currency
Now that we possess a basic understanding of how SMPC operates, how might we apply it to construct a decentralized currency engine? The conventional description of a blockchain in this blog is as a system that sustains a state, S, accepts transactions, reaches consensus on which transactions should be executed at a certain time, and computes a state transition function APPLY(S, TX) -> S’ OR INVALID. In this context, we will assert that all transactions are deemed valid, and if a transaction TX is invalid, then we simply conclude that APPLY(S, TX) = S.
Given that the blockchain lacks transparency, we might anticipate the requirement for two different categories of transactions that users can submit into the SMPC: get requests, inquiring about specific details regarding an account in the present state, and update requests, comprising transactions to enact on the state. We will establish the rule that each account can solely request balance and nonce details pertaining to itself, and can only withdraw from its own balance. We characterize the two types of requests as follows:
SEND: [from_pubkey, from_id, to, value, nonce, sig] GET: [from_pubkey, from_id, sig]
The information is preserved across the N nodes in the subsequent structure:
In essence, the information is organized as a collection of 3-tuples that symbolize accounts, with each 3-tuple encapsulating the owning pubkey, nonce, and balance. To initiate a request, a node formulates the transaction, partitions it into secret shares, creates a random request ID, and appends both the ID and a minor amount of proof of work to each share. The proof of work is essential due to the requirement for some anti-spam strategies, and since account balances are confidential, there’s no means to ascertain if the sending account possesses sufficient funds to cover a transaction fee. The nodes then autonomously validate the shares of the signature against the portion of the public key provided in the transaction (there exist signature methodologies permitting this sort of share-by-share validation; Schnorr signatures represent one significant category). If any specific node encounters an invalid share (due to proof of work or signature issues), it discards it; otherwise, it accepts it.
Accepted transactions are not executed instantaneously, akin to a blockchain framework; initially, they are stored within a memory pool. Every 12 seconds, we employ a consensus algorithm – it might be a straightforward approach, such as a random node from the N acting as a dictator, or a sophisticated neo-BFT algorithm similar to that utilized by Pebble – to reach a consensus on which set of request IDs should be processed and in what sequence (for ease, basic alphabetical ordering will likely be adequate).
At this point, to fulfill a GET request, the SMPC will perform computations and reconstruct the result of the following operation:
owner_pubkey = R[0] * (from_id == 0) + R[3] * (from_id == 1) + ... + R[3*n] * (from_id == n) valid = (owner_pubkey == from_pubkey) output = valid * (R[2] * (from_id == 0) + R[5] * (from_id == 1) + ... + R[3n + 2] * (from_id == n))
What is the purpose of this equation? It is structured in three phases. Initially, we obtain the owner pubkey of the account for which the request seeks to ascertain the balance. Since the calculation occurs within an SMPC, and therefore no node is aware of the specific database index to access, we achieve this by simply collecting all database indices, multiplying the unrelated ones by zero and then computing the total. Following this, we verify if the request is attempting to acquire information from an account that it indeed possesses (recall that we verified the legitimacy of from_pubkey against the signature in the initial phase, thus here we merely require to confirm the account ID against the from_pubkey). Ultimately, we apply the same database retrieval primitive to obtain the balance, and multiply the balance by the validity to derive the outcome (i.e., invalid requests yield a balance of 0, while valid ones reflect the actual balance).
Now, let’s examine the process of a SEND operation. First, we calculate the validity condition, which entails verifying that (1) the public key of the targeted account is accurate, (2) the nonce is appropriate, and (3) the account possesses sufficient funds for the transaction. It is important to note that to accomplish this we again employ the “multiply by an equality check and add” protocol, but for simplicity, we will shorten R[0] * (x == 0) + R[3] * (x == 1) + … to R[x * 3].
valid = (R[from_id * 3] == from_pubkey) * (R[from_id * 3 + 1] == nonce) * (R[from_id * 3 + 2] >= value)
Next, we proceed with:
R[from_id * 3 + 2] -= value * valid R[from_id * 3 + 1] += valid R[to * 3 + 2] += value * valid
As for database updates, R[x * 3] += y translates to the subsequent set of commands R[0] += y * (x == 0), R[3] += y * (x == 1) …. It should be noted that all of these can be executed in parallel. Furthermore, keep in mind that for the implementation of balance verification we utilized the >= operator. This, once again, is trivial through the use of boolean logic gates; however, even when applying a finite field for optimization, there do exist some ingenious methods for executing the verification using solely additions and multiplications.
In all of the preceding points, we identified two primary constraints regarding efficiency within the SMPC framework. Initially, accessing and modifying a database incurs an O(n) expense since you essentially have to examine and alter every cell. Doing less would entail revealing to individual nodes which segment of the database a read or write originated from, potentially causing statistical memory leaks. Secondly, each multiplication necessitates a network communication, leading to the realization that the critical limitation here is not computation or memory, but latency. Hence, it becomes evident that secret sharing networks are regrettably not ideal protocols; while they can efficiently manage business logic, they will never handle anything more intricate – even cryptographic verifications, apart from a select few specifically designed for the platform, are often too costly.
Transitioning from Currency to EVM
Now, the subsequent challenge is determining how to transition from this basic toy currency to a standard EVM processor. Let’s delve into the code for the virtual machine operating within a solitary transaction framework. A more straightforward version of the function appears roughly as follows:
def run_evm(block, tx, msg, code): pc = 0 gas = msg.gas stack = [] stack_size = 0 exit = 0 while 1: op = code[pc] gas -= 1 if gas 0 or stack_size get_stack_req(op): exit = 1 if op == ADD: x = stack[stack_size] y = stack[stack_size - 1] stack[stack_size - 1] = x + y stack_size -= 1 if op == SUB: x = stack[stack_size] y = stack[stack_size -```html 1] pile[pile_size - 1] = x - y pile_size -= 1 ... if op == JUMP: pc = pile[pile_size] pile_size -= 1 ...
The parameters involved are:
- The script
- The pile
- The memory
- The account status
- The program pointer
Therefore, we can merely save these as records, and for each computational step execute a function akin to the following:
op = script[pc] * alive + 256 * (1 - alive) gas -= 1 pile_p1[0] = 0 pile_p0[0] = 0 pile_n1[0] = pile[pile_size] + pile[pile_size - 1] pile_sz[0] = pile_size - 1 new_pc[0] = pc + 1 pile_p1[1] = 0 pile_p0[1] = 0 pile_n1[1] ``````html = stack[stack_size] - stack[stack_size - 1] stack_sz[1] = stack_size - 1 new_pc[1] = pc + 1 ... stack_p1[86] = 0 stack_p0[86] = 0 stack_n1[86] = stack[stack_size - 1] stack_sz[86] = stack_size - 1 new_pc[86] = stack[stack_size] ... stack_p1[256] = 0 stack_p0[256] = 0 stack_n1[256] = 0 stack_sz[256] = 0 new_pc[256] = 0 pc = new_pc[op] stack[stack_size + 1] = stack_p1[op] stack[stack_size] = stack_p0[op] stack[stack_size - 1] ``````html = stack_n1[op] stack_size = stack_sz[op] pc = new_pc[op] alive *= (gas 0) * (stack_size 0)
Fundamentally, we determine the outcome of every single opcode concurrently, and subsequently select the appropriate one to alter the state. The alive parameter initializes at 1, and if at any stage the alive parameter turns to zero, all actions from that moment effectively cease to operate. This appears to be extraordinarily inefficient, which it is, yet keep in mind: the constraint is not processing time but delay. All of the preceding can be parallelized. Indeed, the observant reader might realize that the overall operation of executing every opcode concurrently possesses only O(n) complexity in terms of the number of opcodes (especially if earlier we capture the top several elements of the stack into designated variables for both input and output, which for simplicity we have not done), thus it isn’t even the most computationally demanding segment (if the number of accounts or storage slots surpasses that of opcodes, which seems plausible, database updates are). At the conclusion of every N cycles (or for reduced information leakage every power of two of cycles), we reconstruct the alive parameter, and upon observing that alive = 0, we terminate.
In an EVM with numerous stakeholders, the database is likely to be the most substantial burden. To alleviate this challenge, there are potentially clever trade-offs regarding information leakage that can be implemented. For instance, we already acknowledge that most often code is retrieved from sequential database indices. Thus, one potential method could involve storing the code as a series of large integers, each large integer encapsulating several opcodes, and then employing bit decomposition protocols to extract individual opcodes from a number upon loading it. There are probably many methods to enhance the virtual machine’s fundamental efficiency; the prior discussion is intended, once again, as proof of concept to demonstrate that a secret sharing DAO is inherently achievable, not anything resembling an optimal execution. Moreover, we can explore architectures akin to those utilized in scalability 2.0 strategies to significantly compartmentalize the state to further elevate efficiency.
Modifying the N
The SMPC framework described previously presumes the presence of existing N parties and aspires to remain secure against any minority of them (or in certain configurations at least any minority less than 1/4 or 1/3) colluding. Nonetheless, blockchain protocols must theoretically endure indefinitely, thus stagnant economic groups cannot be sustained; instead, we must select the consensus participants through a mechanism like proof of stake. A potential protocol might function as follows:
- The secret sharing DAO’s time is segmented into “epochs”, each potentially spanning between an hour and a week.
- In the initial epoch, the participants are designated as the top N stakeholders from the genesis sale.
- At the conclusion of an epoch, anyone can register to be among the participants in the subsequent round by placing down a deposit. N participants are randomly selected, and disclosed.
- A “decentralized handoff protocol” is executed, where the N participants concurrently distribute their shares among the incoming N, and each of the new N reconstitutes their share from the segments they received – effectively, the same protocol utilized for multiplication. It is important to note that this protocol can also adjust the number of participants up or down.
Everything above deals with decentralization under the assumption of honest participants; however, within a cryptocurrency protocol, we also require incentives. To achieve this, we utilize a collection of primitives referred to as verifiable secret sharing, which enable us to ascertain if a given node acted honestly during the secret sharing phase. Essentially, this method operates by conducting the secret sharing computations in parallel across two distinct levels: utilizing integers and employing elliptic curve points (other constructions also exist, but since cryptocurrency users are most familiar with the secp256k1 elliptic curve, we will utilize that). Elliptic curve points are advantageous because they have a commutative and associative addition operator – in essence, they are extraordinary objects which can be added and subtracted much like numerical values. One can convert a number into a point, but not vice versa, and we possess the property that number_to_point(A + B) = number_to_point(A) + number_to_point(B). By executing the secret sharing mathematics on both the number level and the elliptic curve point level simultaneously, and making the elliptic curve points public, it becomes feasible to verify any misconduct. For effectiveness, we could likely adopt a Schellingcoin-style protocol to empower nodes to penalize other nodes that are dishonest.
Use Cases
So, what do we possess? If the blockchain acts as a decentralized computer, then a secret sharing DAO serves as a decentralized computer with confidentiality. The secret sharing DAO incurs significant costs for this additional feature: a network message is imperative for each multiplication and each database access. As
“`a consequence, gas expenses are expected to be significantly more elevated than Ethereum itself, restricting the processing to primarily basic business logic and preventing the application of various cryptographic computations. Scalability solutions may be utilized to somewhat alleviate this limitation, but there will ultimately be constraints on how far this can extend. Therefore, this technology is likely not to be applicable for every scenario; rather, it will function more like a specialized kernel intended for specific types of decentralized applications. Illustrative cases include:
- Medical documentation – maintaining data on a secure decentralized platform could potentially facilitate an intuitive and safe health information system that empowers patients to control their data. Notably, proprietary diagnostic algorithms could operate within the secret sharing DAO, enabling medical diagnosis as a service based on data from different medical examination firms without jeopardizing the risk of unintentional or intentional exposure of your private information to insurers, advertisers, or other companies.
- Private key custody – a decentralized M-of-N substitute for centralized password recovery; applicable for both financial and non-financial uses
- Multisignature for any application – even systems that do not inherently support arbitrary access policies, or even M-of-N multisignature accessibility, will now support them, provided they utilize cryptography, since the private key can be contained within a secret sharing DAO.
- Reputation frameworks – consider the possibility of reputation scores being kept within a secret sharing DAO, allowing you to grant reputation to other users privately, and have your rating contribute to that user’s overall reputation, without anyone being able to view your specific ratings?
- Confidential financial networks – secret sharing DAOs could offer an alternative pathway to Zerocash-style completely anonymous currency, but with the added capability that functionality could be more readily expanded to decentralized exchanges and sophisticated smart contracts. Business entities may want to harness some advantages of operating their enterprises atop crypto without necessarily disclosing every aspect of their internal operations to the general audience.
- Matchmaking algorithms – connect employers, employees, dating partners, drivers for your next ride on Decentralized Uber, etc., while performing the matchmaking algorithm computations within SMPC so that no one accesses any of your information unless the algorithm confirms that you are an ideal match.
In essence, one could perceive SMPC as providing a collection of tools somewhat akin to those theorized to be supplied by cryptographically secure code obfuscation, with one critical difference: it effectively operates on human-practical time scales.
Additional Consequences
Beyond the aforementioned applications, what additional implications will secret sharing DAOs introduce? Moreover, are there any concerns to address? As it happens, similar to blockchains themselves, a few issues arise. The foremost, and most apparent, challenge is that secret sharing DAOs will significantly expand the range of applications that can be performed entirely privately. Many proponents of blockchain technology often build a considerable part of their case on the crucial observation that while blockchain-based currencies provide unmatched anonymity by not linking addresses to personal identities, they also represent the most transparent form of currency globally, as every transaction appears on a shared ledger. In this context, however, the former remains intact while the latter vanishes completely. What we retain is effectively complete anonymity.
If this level of anonymity results in a substantial increase in illicit activities, and the public finds the tradeoffs unacceptable, we might anticipate that governments and various institutions, perhaps even joined by volunteer hacker vigilantes, will endeavor to dismantle these systems, and they might even be justified in doing so. Fortunately for these adversaries, secret sharing DAOs have an unavoidable vulnerability: the 51% attack. If 51% of the maintainers of a secret sharing DAO at any given time decide to conspire, they can uncover any of the information under their authority. Additionally, this power is not bound by any statute of limitations: if a group of entities who once constituted over half of the maintaining team of a secret sharing DAO colludes years later, they can still expose information from that earlier period. In conclusion, if society strongly opposes any actions within a secret sharing DAO, there will be numerous opportunities for the operators to collaborate to halt or disclose what’s occurring.
A secondary, and more nuanced, concern relates to how the concept of secret sharing DAOs undermines a cherished notion in cryptoeconomics: that private keys are not securely tradable. Many protocols explicitly or implicitly rely on this principle, including non-outsourceable proof of work puzzles, Vlad Zamfir and Pavel Kravchenko’s proof of custody, economic frameworks that treat private keys as identities, and any kind of economic status aimed to be untradeable, etc. Online voting systems frequently require that it should be impossible to demonstrate that you voted with a particular key to prevent vote selling; with secret sharing DAOs, the issue is that now you can indeed sell your vote, and quite easily: simply by placing your private key into a contract within a secret sharing DAO and leasing out access.
The implications of this capability to sell private keys are extensive – in fact, they almostthreaten the integrity of the most robust system securing blockchain: proof of stake. The potential concern is as follows: proof of stake derives its security from users having security deposits on the blockchain, which can potentially be revoked if a user misbehaves in some manner (such as double-voting, voting for a fork, abstaining entirely, etc). Here, as private keys become tradeable, security deposits become tradeable as well. We must pose the question: does this jeopardize proof of stake?
Fortunately, the response is no. Firstly, there are strong lemon-theoretic justifications for why no individual would genuinely desire to dispose of their deposit. Should you possess a deposit of $10, to you it represents $10 less the minimal risk of a potential hack. However, if you attempt to transfer that deposit to another person, they will consider a deposit worth $10, unless you opt to utilize your private key to cast two votes and effectively nullify the deposit. Therefore, from their perspective, there exists a persistent looming danger that you might take away their deposit, and you personally have no motivation to refrain from doing so. The mere action of attempting to sell your deposit should raise their concerns. Thus, from their view, your deposit might be valued at perhaps $8. You have no justification to forfeit $10 for $8, so as a logical agent, you would retain the deposit for yourself.
Secondly, if the private key was held within the secret sharing DAO from the very beginning, transferring access to the key would mean that you would forfeit your access to it. Consequently, you would effectively transfer both authority and responsibility simultaneously – from an economic perspective, the outcome would be identical to if one of the deposit holders merely experienced a change in identity at some point during the procedure. In reality, secret sharing DAOs could even enhance the proof of stake system by providing a safer platform for participants involved in decentralized stake pools, even within protocols such as Tendermint, which do not natively support that functionality.
There exist additional reasons why the theoretical assaults enabled by secret sharing DAOs might indeed falter in practice. For instance, consider the situation of non-outsourceable puzzles, computational challenges aimed at demonstrating ownership of both a private key and a piece of information simultaneously. One specific implementation of a non-outsourceable puzzle, utilized by Permacoin, involves a computation that must “bounce” back and forth between the key and the information hundreds of thousands of times. This is manageable when both pieces of data reside on the same piece of hardware, but becomes unfeasibly slow if separated by a network connection – and over a secret sharing DAO, the inefficiencies would render it nearly impossible. Consequently, one potential inference from this is that secret sharing DAOs will result in the standardization of a signature scheme that necessitates several hundred million rounds of computation – ideally featuring extensive serial multiplication – to execute, at which stage every computer, mobile device, or internet-of-things microchip would possess a built-in ASIC to perform it effortlessly, leaving secret sharing DAOs behind, and allowing us all to progress with our lives.
How Far Away?
What remains before secret sharing DAO technology can achieve mainstream adoption? In summary, quite a bit, but not overly much. Initially, there is undoubtedly a moderate degree of technical engineering necessary, particularly at the protocol level. Someone must establish a formal SMPC implementation, along with its integration into an EVM framework, likely with multiple constraints for efficiency (for instance, hash functions within SMPC are extremely costly, leading to the potential disappearance of Merkle tree storage in favor of every contract maintaining a limited number of storage slots), and a punitive, incentive, and consensus structure with a hypercube-style scalability model, followed by releasing the protocol specifications. From that juncture, it would take a few months of development in Python (Python should suffice, as the primary bottleneck will be network latency, not computational power), and a working proof of concept would be achieved.
Secret sharing and SMPC technologies have existed for multiple years, and academic cryptographers have discussed how to create privacy-preserving applications using M-of-N-based primitives and related technologies, such as private information retrieval, for over a decade. The significant contribution made by Bitcoin, however, is the notion that M-of-N frameworks, in general, can be significantly more easily initiated if an economic layer is included. A secret sharing DAO equipped with an integrated currency would incentivize individuals to engage in network maintenance, facilitating the process until it becomes entirely self-sustaining through internal applications. Thus, collectively, this technology is very feasible and not nearly as distant; it is merely a matter of time before someone realizes it.

