Special acknowledgments to Vlad Zamfir and Jae Kwon for several of the concepts detailed in this article
Beyond the central discussion on weak subjectivity, a significant secondary point raised against proof of stake is the challenge that proof of stake algorithms are considerably more complex to make light-client accessible. In contrast to proof of work algorithms, which entail the generation of block headers that can be swiftly confirmed, permitting a relatively compact chain of headers to serve as an implicit verification that the network regards a specific history as valid, proof of stake is more difficult to integrate into such a structure. Since the legitimacy of a block in proof of stake hinges on stakeholder signatures, it is contingent on the ownership distribution of the currency within the specific block that was endorsed, which appears to indicate, at least initially, that to achieve any confidence in the legitimacy of a block, the entire block must be authenticated.
Given the critical significance of light client protocols, particularly considering the recent corporate interest in “internet of things” technologies (which frequently have to operate on very weak and low-power devices), the feature of light client compatibility is essential for a consensus algorithm, and thus an efficient proof of stake framework must tackle this issue.
Light Clients in Proof of Work
Generally, the fundamental motivation for the “light client” idea is as follows. Alone, blockchain protocols, with the stipulation that each node must handle every transaction to maintain security, are costly, and as a protocol gains significant popularity, the blockchain size grows so vast that numerous users become incapable of sustaining that cost. The Bitcoin blockchain is presently 27 GB in size, and thus very few participants choose to keep running “full nodes” that process every transaction. On smartphones, and notably on embedded systems, running a full node is simply unfeasible.
Therefore, it is vital to have a method for users with significantly lesser computational capabilities to still obtain secure assurances regarding various aspects of the blockchain state – such as the balance/state of a certain account, whether a specific transaction was processed, if a certain event took place, etc. Ideally, a light client should be able to accomplish this in logarithmic time – meaning, squaring the number of transactions (for example, increasing from 1000 tx/day to 1000000 tx/day) should only double a light client’s expenses. Fortunately, it is indeed feasible to construct a cryptocurrency protocol that can be securely evaluated by light clients with such efficiency.
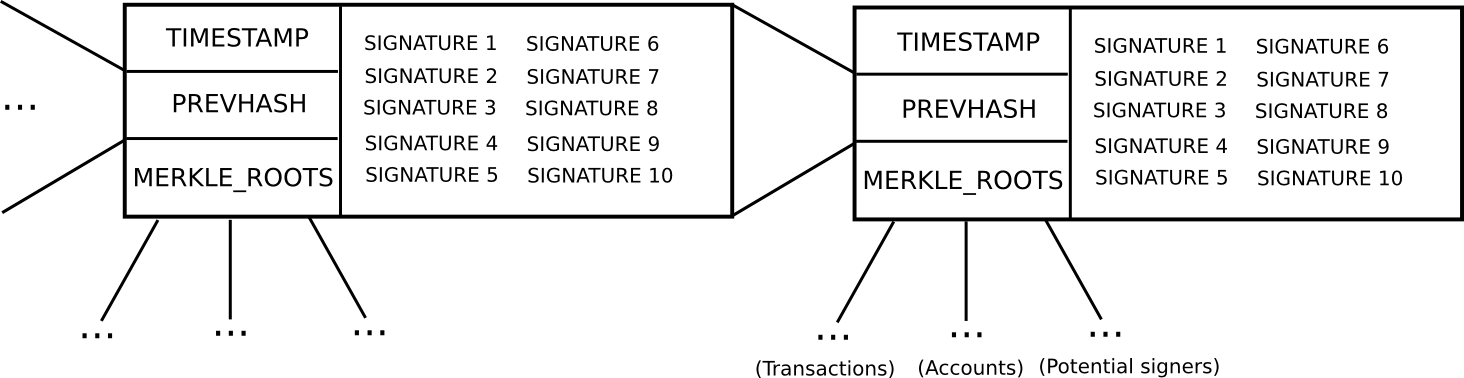
Basic block header framework in Ethereum (note that Ethereum incorporates a Merkle tree for transactions and accounts in each block, enabling light clients to easily access more data)
In Bitcoin, light client security functions as follows. Instead of forming a block as a single comprehensive unit containing all transactions directly, a Bitcoin block is divided into two segments. First, there is a compact data element known as the block header, encompassing three essential pieces of information:
- The hash of the preceding block header
- The Merkle root of the transaction tree (see below)
- The proof of work nonce
Other information like the timestamp is also included in the block header, but this is not pertinent here. Second, there exists the transaction tree. Transactions within a Bitcoin block are stored in a data structure referred to as a Merkle tree. The nodes at the lowest level of the tree represent the transactions, and as one moves upward, each node is the hash of its two subordinate nodes. For instance, if the lowest level contained sixteen transactions, then the next level would have eight nodes: hash(tx[1] + tx[2]), hash(tx[3] + tx[4]), etc. The level above would contain four nodes (for example, the first node equates to hash(hash(tx[1] + tx[2]) + hash(tx[3] + tx[4]))), the level above has two nodes, and then the apex has one node, the Merkle root of the complete tree.
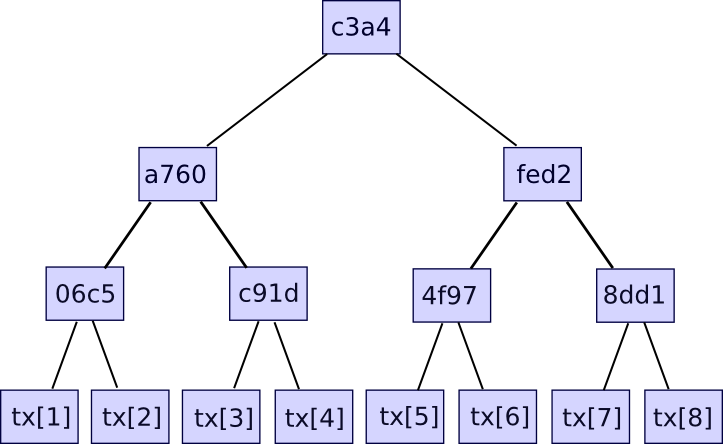
The Merkle root can be viewed as a hash of all transactions combined, and possesses the same attributes expected from a hash – if even a single bit in a transaction is altered, the Merkle root will change entirely, and it is impossible to conceive two different sets of transactions that yield the same Merkle root. The necessity for this more intricate tree structure is that it provides a compact method to prove that a certain transaction was included in a specific block. How? Essentially, one simply needs to present the branch of the tree leading down to the transaction:
The verifier will check only the hashes proceeding down along the branch, assuring that the given transaction is indeed a member of the tree responsible for producing a specific Merkle root. Should an attacker attempt to modify any hash along the branch, the hashes will cease to align and the proof will be rendered invalid. The proof’s size corresponds to the tree’s depth – that is, logarithmic in relation to the transaction count. If your block consists of 220 (i.e., ~1 million) transactions, then the Merkle tree will comprise only 20 levels, meaning the verifier will only need to compute 20 hashes to validate a proof. If your block includes 230 (i.e., ~1 billion) transactions, then the Merkle tree will consist of 30 levels, allowing a light client to verify a transaction with merely 30 hashes.
Ethereum enhances this fundamental mechanism with two additional Merkle trees in each block header, empowering nodes to validate not solely that a specific transaction took place but also that a particular account possesses a certain balance and state, that a certain event transpired, and even that a specific account does not exist.
Validating the Roots
Currently, this transaction validation procedure presupposes a single factor: that the Merkle root is reliable. If an individual demonstrates that a transaction is a component of a Merkle tree associated with a particular root, that alone carries no weight; belonging to a Merkle tree only verifies a transaction’s legitimacy if the Merkle root itself is acknowledged as legitimate. Thus, another vital aspect of a light client protocol involves determining precisely how to authenticate the Merkle roots – or, more broadly, how to verify the block headers.
Firstly, let’s clarify what we mean by “validating block headers”. Light clients are unable to fully authenticate a block on their own; collaborative protocols exist for performing validation, but this method is resource-intensive, so to avert adversaries from squandering everyone’s time with invalid blocks, we require a mechanism to swiftly ascertain whether a specific block header is likely valid. By “likely valid”, we mean this: if an assailant provides us with a block deemed likely valid, but which is not genuinely valid, then the assailant must incur significant costs for doing so. Even if the assailant temporarily deceives a light client or squanders its time, they should still incur greater losses than the victims of the attack. This is the standard we will enforce across both proof of work and proof of stake.
In proof of work, the method is straightforward. The fundamental concept behind proof of work is that there exists a mathematical formula that a block header must fulfill to be deemed valid, and generating such a valid header is computationally demanding. When a light client has been offline for a certain period and reconnects, it will seek out the longest sequence of valid block headers, assuming that this sequence represents the authentic blockchain. The expense involved in spoofing this system—by providing a sequence of block headers that is likely-valid-but-not-actually-valid—is exceedingly high; in fact, it is almost identical to the cost of initiating a 51% attack on the network.
In Bitcoin, this proof of work requirement is straightforward: sha256(block_header) (in reality, the “target” value fluctuates, but we can exclude this from our simplified evaluation). To meet this requirement, miners must continually attempt various nonce values until they encounter one that satisfies the proof of work criteria for the block header; on average, this requires about 269 computational effort per block. The brilliant aspect of Bitcoin-style proof of work is that each block header can be independently verified without depending on any outside information at all. This implies that the process of validating block headers can indeed be executed in constant time – download 80 bytes and compute a hash of it – even superior to the logarithmic limit we’ve set for ourselves. Regrettably, in proof of stake, such an elegant mechanism does not exist.
Light Clients in Proof of Stake
To establish an effective light client for proof of stake, ideally, we wish to accomplish the same complexity-theoretic properties as proof of work, albeit through a different approach. Once a block header is deemed trustworthy, the method for accessing any data from the header remains consistent, so we understand it will require a logarithmic time to accomplish. However, we aim to ensure the process of validating the block headers themselves is also logarithmic.
To initiate, let us outline an earlier version of Slasher, which was not specifically crafted to be light-client optimal:
- To qualify as a “potential block producer” or “potential signer,” a user is required to stake a security deposit of a determined size. This security deposit can be made at any moment and remains valid for an extended timeframe, say 3 months.
- During each time slot T (for example, T = 3069120 to 3069135 seconds post-genesis), a certain function generates a random number R (numerous complexities are involved in ensuring the random number is secure, but they are not pertinent here). Then, suppose the potential signer set ps (stored in a distinct Merkle tree) has size N. We select ps[sha3(R) % N] as the block producer, and ps[sha3(R + 1) % N], ps[sha3(R + 2) % N] … ps[sha3(R + 15) % N] as the signers (essentially, employing R as entropy to randomly select a signer and 15 block producers)
- Blocks are composed of a header containing (i) the hash of the prior block, (ii) the compilation of signatures from the block producer and signers, (iii) the Merkle root of the transactions and state, alongside (iv) additional data such as the timestamp.
- A block created during time slot T is considered valid if that block is signed by the block producer and at least 10 of the 15 signers.
- If a block producer or signer actively partakes in the block production process, they receive a modest signing reward.
- Should a block producer or signer endorse a block that is not part of the main chain, then that signature may be submitted into the main chain as “proof” that the block producer or signer is attempting to engage in an attack, resulting in that block producer or signer forfeiting their deposit. The evidence submitter may gain 33% of the deposit as a reward.
In contrast to proof of work, where the motivation not to mine on a fork of the primary chain is the missed opportunity of not receiving the reward on the main chain, in proof of stake, the incentive is that if you mine on the incorrect chain, you will face explicit penalties for it. This is crucial; because a substantial amount of penalties can be imposed for each incorrect signature, a significantly smaller quantity of block headers is necessary to provide the same security margin.
Now, let’s analyze what a light client must accomplish. Suppose the light client was last online N blocks prior and seeks to validate the state of the current block. What processes must the light client undertake? If a light client is already aware that a block B[k] is genuine and wishes to authenticate the subsequent block B[k+1], the steps are approximately as follows:
- Calculate the function that produces the random value R during block B[k+1] (computable in either constant or logarithmic time dependingon execution)
- Given R, retrieve the public keys/addresses of the chosen blockmaker and signer from the blockchain’s state tree (logarithmic time)
- Authenticate the signatures in the block header against the public keys (constant time)
And that’s all. There’s a slight nuance, however. The group of possible signers may change throughout the block, suggesting that a light client could need to process the transactions in the block prior to calculating ps[sha3(R + k) % N]. Nevertheless, we can address this by simply stating that it’s the initial signer set from the beginning of the block, or even from a block 100 blocks earlier, that we are making selections from.
Now, let’s determine the formal security guarantees provided by this protocol. Imagine a light client processes a series of blocks, B[1] … B[n], where all blocks commencing from B[k + 1] are invalid. Assuming that all blocks preceding B[k] are valid, and that the signer set for block B[i] is derived from block B[i – 100], this implies that the light client will accurately infer the signature authenticity for blocks B[k + 1] … B[k + 100]. Thus, if an adversary creates a set of fraudulent blocks that deceive a light client, the light client can still be confident that the attacker will need to forfeit ~1100 security deposits for the first 100 invalid blocks. For subsequent blocks, the adversary might manage to sign blocks with false addresses, but 1100 security deposits provide ample assurance, especially since the deposits can vary in size, potentially encompassing millions of dollars in total.
Therefore, even this earlier iteration of Slasher adheres to our definition of being light-client-friendly; we can achieve equivalent security assurances as with proof of work in logarithmic time.
An Improved Light-Client Protocol
Nonetheless, we can greatly enhance the basic algorithm mentioned above. The pivotal realization that propels us further is the concept of partitioning the blockchain into epochs. Here, we will articulate a more sophisticated iteration of Slasher, which we’ll refer to as “epoch Slasher.” Epoch Slasher mirrors the previous Slasher but introduces a few additional stipulations:
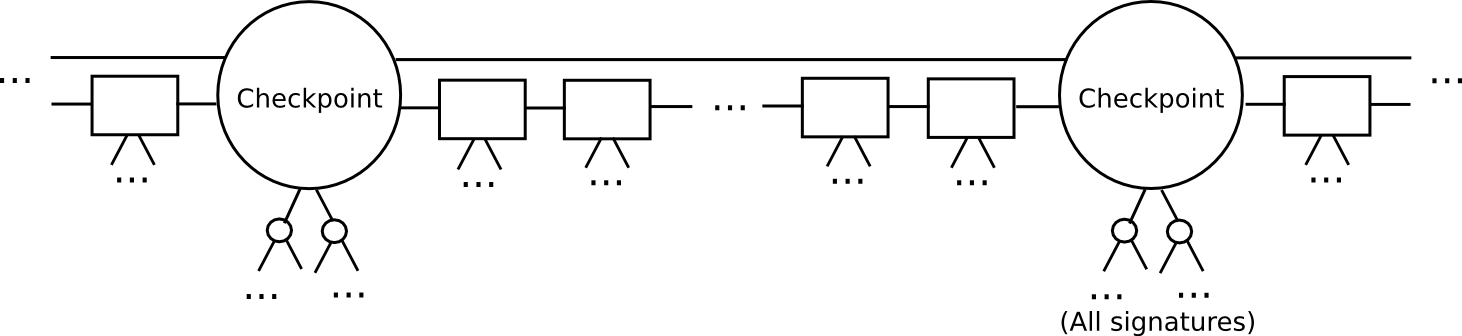
- Define a checkpoint as a block such that block.number % n == 0 (i.e., every n blocks includes a checkpoint). Consider n to be approximately a few weeks; it only needs to be significantly less than the duration of the security deposit.
- For a checkpoint to be deemed valid, two-thirds of all potential signers must endorse it. Furthermore, the checkpoint needs to explicitly incorporate the hash of the preceding checkpoint.
- The signer set during a non-checkpoint block ought to be established from the signer set of the second-to-last checkpoint.
This protocol enables a light client to catch up considerably quicker. Rather than processing every block, the light client could jump directly to the next checkpoint and validate it. The light client can even probabilistically verify the signatures by randomly selecting 80 signers and specifically requesting signatures from them. If those signatures are found invalid, then we can be statistically assured that countless security deposits are likely to be lost.
Once a light client has authenticated up to the most recent checkpoint, it can simply acquire the latest block and its 100 predecessors, employing a more straightforward per-block protocol to validate them as per the original Slasher; if those blocks turn out to be invalid or part of the wrong chain, given that the light client has already validated the latest checkpoint, and in accordance with the rules of the protocol, it can be assured that the deposits at that checkpoint will remain active until at least the next checkpoint, once again enabling the light client to be confident that at least 1100 deposits will be forfeited.
With this subsequent protocol, we observe that not only is proof of stake equally capable of being light-client friendly as proof of work, but it’s actually even more conducive to light-client operations. With proof of work, a light client synchronizing with the blockchain is required to download and process each block header in the chain, which becomes particularly costly if the blockchain operates rapidly, aligning with one of our design goals. With proof of stake, we can straightforwardly skip to the most recent block and validate the prior 100 blocks to secure an assurance that if we are aligned with the incorrect chain, no less than 1100 security deposits will be forfeited.
Additionally, there remains a valid role for proof of work within proof of stake. As demonstrated, it requires logarithmic effort to potentially validate each individual block in proof of stake, and thus an attacker can still inflict a logarithmic level of disruption on light clients by disseminating invalid blocks. Proof of work by itself can effectively be validated within constant time, and without retrieving any data from the network. Therefore, it may be prudent for a proof of stake algorithm to still mandate a minimal quantity of proof of work for each block, ensuring that an attacker needs to expend some computational resources merely to marginally inconvenience light clients. Nevertheless, the computational resources required for generating these proofs of work should only be minimal.

