Blockchains represent a formidable technology, as consistent followers of the blog likely concur. They facilitate a multitude of interactions to be formalized and executed in a manner that significantly enhances dependability, eliminates business and political dangers linked to the procedure being overseen by a centralized organization, and minimizes the necessity for trust. They establish a foundation where applications from various organizations and even of diverse kinds can function collaboratively, enabling extraordinarily effective and fluid interactions, and provide an audit trail that anyone can verify to ensure that all processes are being executed accurately.
Nonetheless, when I and others engage with companies regarding developing their applications on a blockchain, two primary concerns consistently arise: scalability and confidentiality. Scalability poses a significant challenge; present blockchains, handling 3-20 transactions per second, are vastly inadequate compared to the processing power required to support mainstream payment systems or financial markets, let alone decentralized forums or global micropayment platforms for the Internet of Things. Fortunately, there are solutions, and we are proactively developing a strategy to realize them. The other significant issue that blockchains encounter is confidentiality. Despite the enticing advantages of a blockchain, neither corporations nor individuals are particularly enthusiastic about disclosing all their information on a public registry that can be freely accessed without restrictions by one’s government, foreign governments, family members, colleagues, and business rivals.
Contrary to scalability, the remedies for confidentiality are, in some instances, simpler to implement (although in other cases exceedingly more challenging); many of them are compatible with existing blockchains, yet they are often far less satisfactory. Crafting a “holy grail” technology that allows users to perform everything they currently can on a blockchain, but with confidentiality, is significantly more challenging; instead, developers often find themselves dealing with partial solutions, heuristics, and strategies tailored to provide privacy for specific categories of applications.
The Holy Grail
Initially, let us explore the technologies that are considered holy grails, in that they genuinely promise the transformation of arbitrary applications into entirely privacy-preserving applications, enabling users to take advantage of the security offered by a blockchain, utilizing a decentralized network for transaction processing, while “encrypting” the information in such a manner that, although all computations occur visibly, the inherent “meaning” of the data is thoroughly obscured.
The most advanced technology promising advancements in this realm is, naturally, cryptographically secure obfuscation. Generally, obfuscation refers to the process of transforming any program into a “black box” equivalent, ensuring that the program retains the same “internal logic” and produces identical outputs for the same inputs, while making it impossible to discern additional details regarding the functionality of the program.
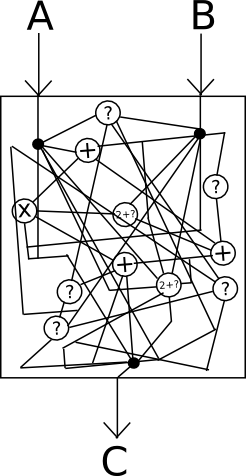
Imagine it as “encrypting” the wires within the box in such a way that the encryption neutralizes itself, ultimately having no effect on the output, yet rendering it utterly impossible to observe the internal workings.
Regrettably, achieving absolutely perfect black-box obfuscation is mathematically established to be impossible; it turns out that there is always at least something that can be extracted from a program by examining it beyond merely its outputs from a specific input set. However, a less rigorous standard known as indistinguishability obfuscation can be achieved: essentially, given two equivalent programs obfuscated with the algorithm (for example, x = (a + b) * c and x = (a * c) + (b * c)), it becomes impossible to ascertain which of the two outputs originated from which original source. To illustrate how this remains sufficiently powerful for our applications, consider the following two programs:
- y = 0
- y = sign(privkey, 0) – sign(privkey, 0)
One simply returns zero, while the other employs a securely held private key to cryptographically sign a message, performs the identical operation once more, subtracts the (obviously matching) results, and returns zero. Even though one program solely returns zero and the other encompasses and utilizes a cryptographic private key, if indistinguishability holds, then it is evident that the two obfuscated programs cannot be differentiated, meaning that someone with access to the obfuscated program has no capability of extracting the private key – otherwise, that would serve as a means of distinguishing the two programs. That’s a remarkably robust form of obfuscation right there – and we’ve known how to implement it for nearly two years!
So, how can we apply this to a blockchain? Here’s a straightforward method for a digital token. We devise an obfuscated smart contract that contains a private key and accepts instructions encrypted with the corresponding public key. The contract maintains account balances in encrypted storage; if the contract wishes to access the storage, it internally decrypts it, and if it aims to write to storage, it encrypts the desired output before doing so. If an individual seeks to check their account balance, they encode that request as a transaction and simulate it on their local machine; the obfuscated smart contract code will validate the signature on the transaction to determine whether that individual has the right to view the balance, and if so, it will return the decrypted value; otherwise, the code will return an error, preventing the user from extracting the information.
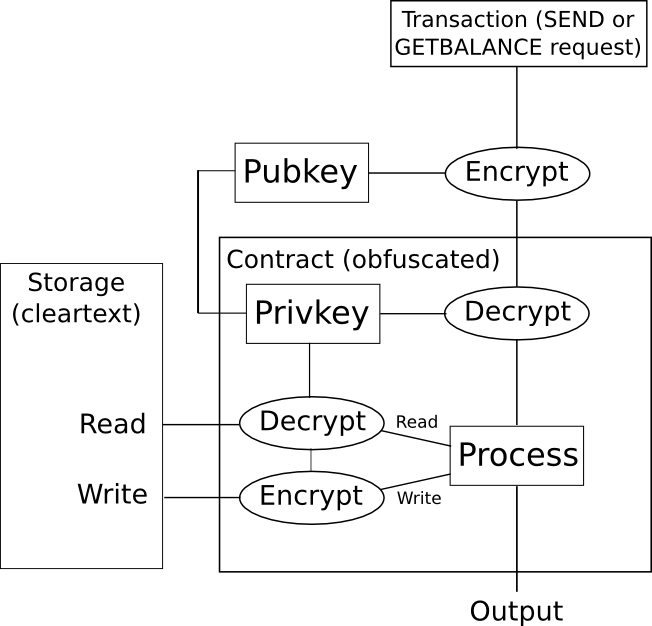
Nevertheless, akin to various other technologies of this nature, one significant issue persists: the process for executing this form of obfuscation is exceptionally inefficient. A billion-factor overhead is commonplace, and often even overly optimistic; a recent study estimates that “executing [a 2-bit multiplication] circuit on the same CPU would take 1.3 * 108 years”. Furthermore, in order to thwart reads and writes to storage from being a vector for data leakage, you must also configure the contract so that read and write actions consistently alter large segments of a contract’s overall state – yet another source of overhead. Adding to that, with the overhead from hundreds of nodes executing the code on a blockchain, it becomes evident how this technology is, regrettably, unlikely to bring about substantial change in the near future.
Taking A Step Down
Nonetheless, there exist two branches of technology that can nearly achieve the level of obfuscation, although with significant compromises to the security framework. The first is secure multi-party computation. Secure multi-party computation enables a program (and its state) to be divided among N participants in such a manner that you require M of them (e.g., N = 9, M = 5) to collaborate to either complete the computation or disclose any internal data within the program or the state. Thus, if you can rely on the majority of the participants to act honestly, the scheme is almost as effective as obfuscation. If you cannot, then it is worthless.
The mathematics behind secure multi-party computation is intricate, yet significantly simpler than obfuscation; if you are interested in the technical aspects, you can explore more here (and also refer to the paper by Enigma, a project that aims to genuinely implement the secret sharing DAO concept, here). SMPC is also considerably more efficient than obfuscation, to the point where practical computations can be performed with it, but even then the inefficiencies are still quite substantial. Addition operations can be processed rather quickly, but every time an SMPC instance executes a small fixed number of multiplication operations, it must execute a “degree reduction” step that involves messages being transmitted from every node to every node within the network. Recent developments have reduced the communication overhead from quadratic to linear, but still, each multiplication operation introduces an unavoidable degree of network latency.
The requirement of trust among participants is also quite burdensome; note that, as is the case with numerous other applications, the participants can save the data and subsequently conspire to uncover it at any future point in time. Additionally, it is impossible to ascertain whether they have done this, making it challenging to incentivize participants to uphold the privacy of the system; for this reason, secure multi-party computation is arguably far better suited to private blockchains, where incentives can derive from outside the protocol, rather than public chains.
Another category of technology that possesses remarkably powerful characteristics is zero-knowledge proofs, particularly the recent advancements in “succinct arguments of knowledge” (SNARKs). Zero-knowledge proofs enable a user to construct a mathematical proof demonstrating that a specified program, when run on some (possibly concealed) input known only to the user, produces a certain (publicly known) output, without disclosing any additional information. There are many specialized varieties of zero-knowledge proofs that are relatively straightforward to implement; for instance, you can consider a digital signature as a type of zero-knowledge proof that indicates you understand the value of a private key which, when processed with a standard algorithm, can be converted into a specific public key. ZK-SNARKs, conversely, allow you to create such a proof for any function.
First, let us examine some concrete examples. One intuitive application for this technology lies in identity systems. For instance, imagine you need to verify to a system that you are (i) a citizen of a specific country, and (ii) above 19 years of age. Suppose your government is technologically progressive, and issues cryptographically signed digital passports, which encompass a person’s name and date of birth, accompanied by a private and public key. You would formulate a function that takes a digital passport and a signature signed by the private key within the passport as input, and returns 1 if (i) the date of birth is prior to 1996, (ii) the passport was signed using the government’s public key, and (iii) the signature is valid, returning 0 otherwise. Subsequently, you would generate a zero-knowledge proof demonstrating that you possess an input which, when processed through this function, yields 1, and sign the proof with another private key intended for your future interactions with this service. The service would then validate the proof, and if correct, it would accept messages signed by your private key as legitimate.
You could also leverage the same scheme to authenticate more intricate claims, such as “I am a citizen of this country, and my ID number does not belong to this set of ID numbers that have already been utilized,” or “I have received positive reviews from certain merchants after spending at least $10,000 on their products,” or “I possess assets valued at a minimum of $250,000”.
Another category of use cases for this technology is digital token ownership. To operate a functional digital token ecosystem, you do not necessarily need transparent accounts and balances; ultimately, what you need is a method to address the “double spending” dilemma – if you own 100 units of an asset, you should be able to utilize those 100 units a single time, not twice. With zero-knowledge proofs, we can certainly accomplish this; the claim that you would zero-knowledge-prove is essentially, “I am aware of a secret number behind one of the accounts in this collection of accounts that have been established, and it does not correspond to any of the secret numbers that have already been disclosed.” In this framework, accounts become one-time-use: an “account” is generated each time assets are transmitted, and the sender account is entirely consumed. If you do not wish to completely deplete a specific account, then you must merely create two accounts, one managed by the recipient and another with the leftover “change” managed by the sender themselves. This is fundamentally the scheme utilized by Zcash (for further details on how it functions, see here).
For two-party smart contracts(for example, envision something akin to a financial derivative agreement negotiated between two entities), the implementation of zero-knowledge-proofs is relatively straightforward. When the agreement is initially formulated, rather than establishing a smart contract containing the actual calculation by which the assets will ultimately be distributed (for instance, in a binary option, the calculation would state “if index I as reported by a data source exceeds X, transfer all to A, otherwise transfer all to B”), establish a contract that contains the hash of the calculation. Upon contract closure, either entity can compute the sum that A and B should obtain and provide this outcome along with a zero-knowledge-proof that a calculation with the appropriate hash yields that outcome. The blockchain determines how much A and B each deposited, and how much they receive, but does not understand the reasons behind their respective deposits or withdrawals.
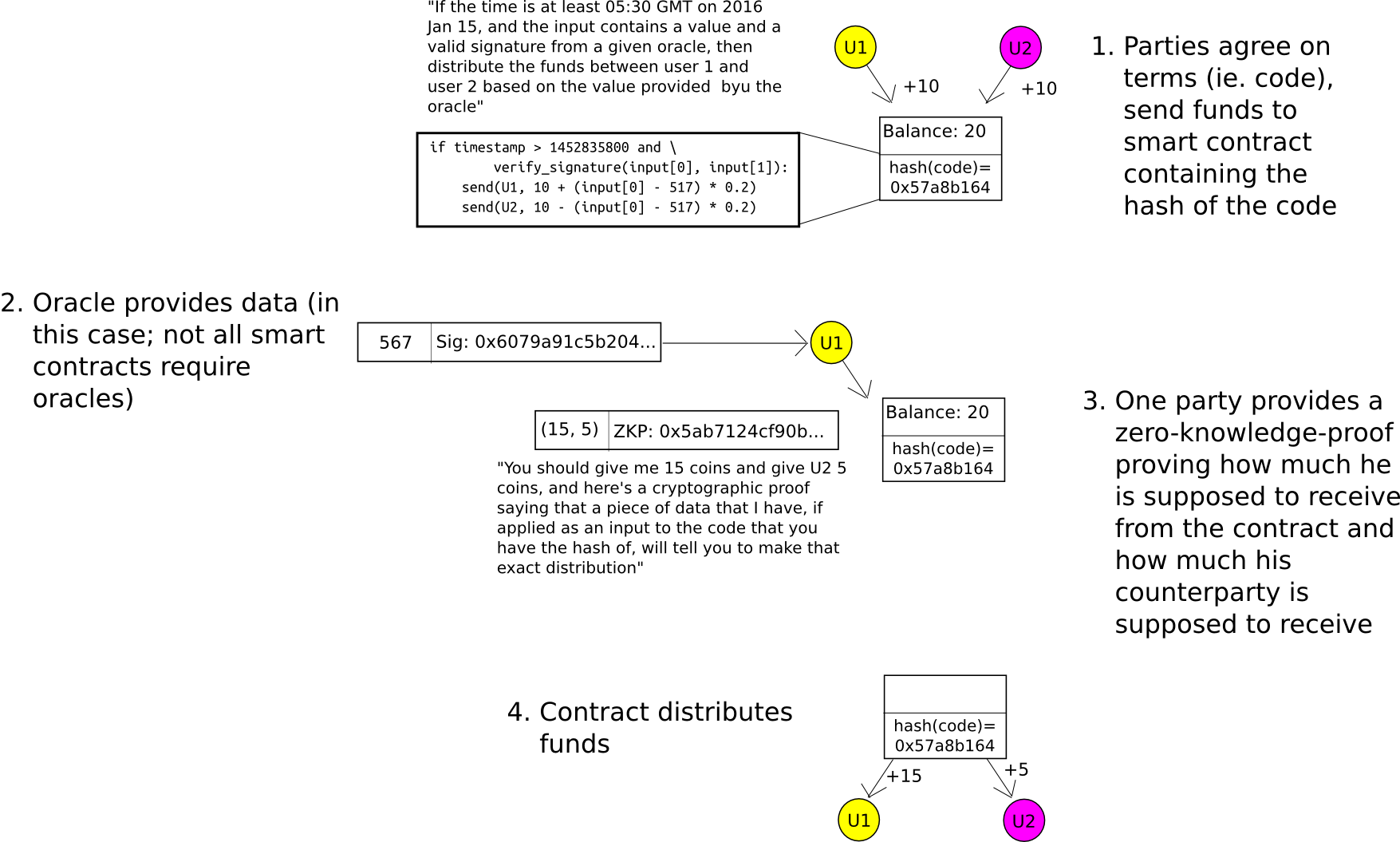
This framework can be extended to N-party smart contracts, and the Hawk initiative is striving to accomplish precisely that.
Beginning from the Opposite Side: Low-Tech Strategies
Another route to enhancing privacy on the blockchain is to initiate with very rudimentary strategies, employing no complex cryptography aside from basic hashing, encryption, and public key cryptography. This represents the approach taken by Bitcoin since its inception in 2009; although the degree of privacy it affords in practice is rather challenging to gauge and restricted, it still evidently offers some advantages.
The most straightforward measure that Bitcoin adopted to somewhat augment privacy is its use of temporary accounts, akin to Zcash, for the purpose of storing funds. Similar to Zcash, every transaction must entirely deplete one or more accounts and generate one or more new accounts, and it is advisable for users to create a new private key for each new account intended for receiving funds (although it is feasible to maintain multiple accounts with the same private key). The primary advantage of this practice is that a user’s assets are not inherently connected to one another: if you receive 50 coins from source A and another 50 coins from source B, there is no way for other individuals to ascertain that these assets belong to the same individual. Furthermore, if you spend 13 coins to someone else’s account C, and then establish a fourth account D where you send the remaining 37 coins from one of these accounts as “change,” other users cannot even discern which of the two outputs from the transaction is the “payment” and which is the “change.”

Nevertheless, there is a challenge. If, at any future moment, you conduct a transaction utilizing funds from two accounts simultaneously, you unavoidably “link” those accounts, making it evident to the public that they originate from a single user. Moreover, these linkages are transitive: should you link A and B at any moment, and subsequently link A and C at another time, and so on, you have generated a considerable amount of evidence that allows for statistical analysis to associate your entire portfolio of assets.

Bitcoin developer Mike Hearn proposed a mitigation strategy known as merge avoidance: essentially, a sophisticated term for earnestly striving to minimize the frequency with which you link accounts through simultaneous spending. This undoubtedly assists, but even so, privacy within the Bitcoin framework has proven to be remarkably porous and heuristic, with no assurances approaching high reliability.
A more sophisticated approach is known as CoinJoin. In essence, the CoinJoin protocol operates as follows:
- N participants convene via an anonymous channel, e.g., Tor. They each supply a destination address D[1] … D[N].
- One participant generates a transaction that dispatches one coin to each destination address.
- The N participants log out and then individually log back into the channel, contributing one coin to the account from which the funds will be dispensed.
- If N coins are credited to the account, they are allocated to the destination addresses; if not, they are refunded.
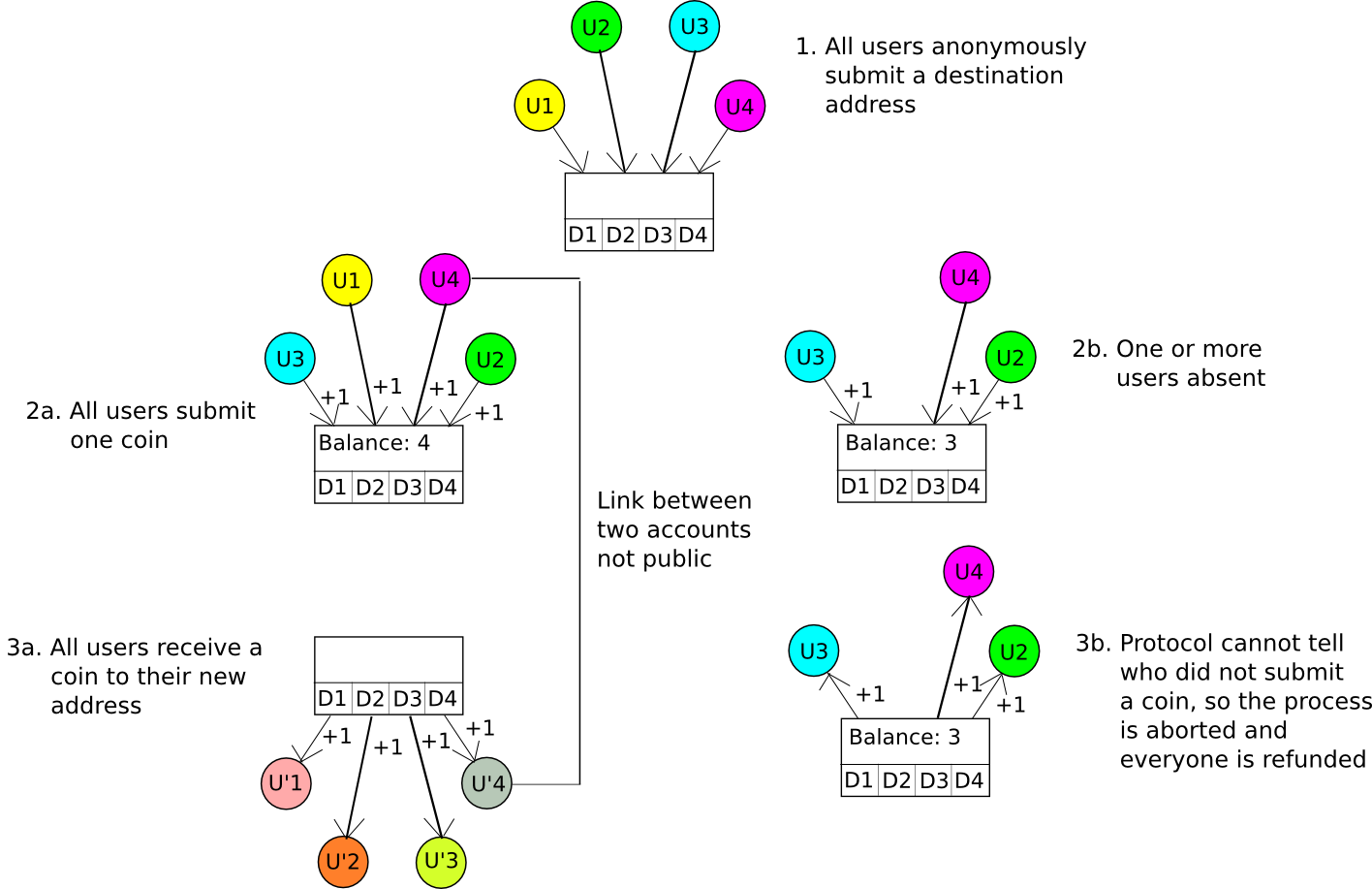
If all participants act honestly and contribute one coin, then everyone will contribute one coin and receive one coin, but nobody will discern which input corresponds to which output. If even a single participant fails to provide their coin, then the process will collapse, the coins will be refunded, and all participants must attempt again. A similar algorithm was executed by Amir Taaki and Pablo Martin for Bitcoin, and by Gavin Wood and Vlad Gluhovsky for Ethereum.
Up to this point, we have solely examined token anonymization. What about two-party smart contracts? In this case, we utilize the same method as Hawk, but we replace the cryptography with more rudimentary cryptoeconomics – specifically, the “auditable computation” approach. Participants send their assets into a contract that retains the hash of the code. When it’s time to distribute the assets, either participant can submit the outcome. The other participant can either issue a transaction to agree on the outcome, permitting the funds to be distributed, or they can unveil the actual code to the contract, at which time the code will execute and allocate the funds appropriately. A security deposit can be employed to encourage the parties to act honestly. Consequently, the system is inherently private, and only in the event of a dispute does any information become accessible to the external world.
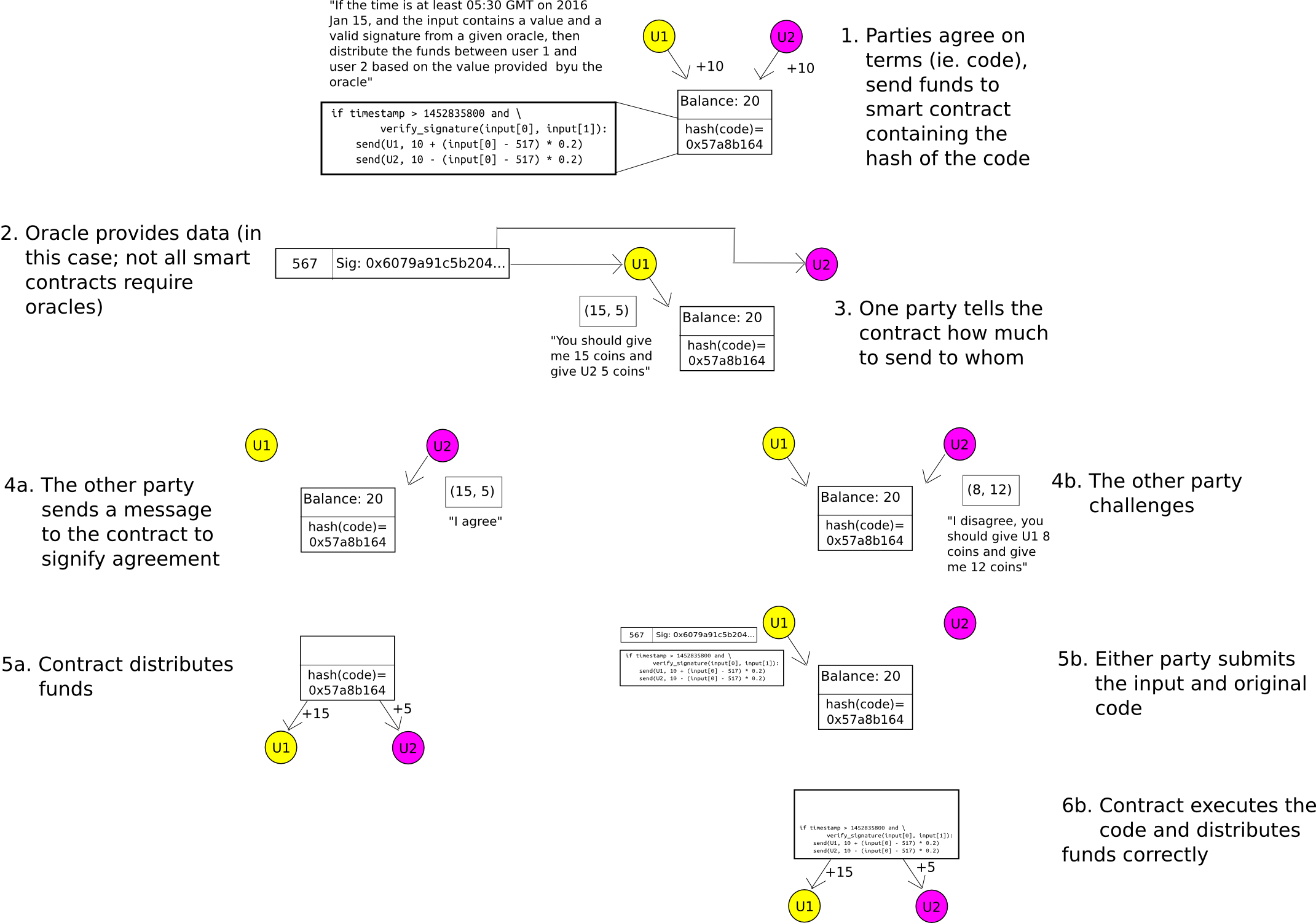
A broadening of this technique is referred to as state channels, and it also presents scalability.benefits in addition to its enhancements in privacy.
Ring Signatures
A technology that is somewhat complex but incredibly promising for both token anonymization and identity use cases is ring signatures. A ring signature fundamentally serves as a verification mechanism that demonstrates the signer possesses a private key linked to a particular set of public keys, without disclosing which one. The brief explanation of the mathematical functioning is that a ring signature algorithm incorporates a mathematical operation that can typically be computed using only a public key, but possessing the private key enables you to introduce a seed to the input, allowing the output to be any specific value you desire. The signature itself includes a sequence of values, each set to the function applied to the preceding value (along with a seed); generating a valid signature necessitates knowledge of a private key to “complete the loop”, ensuring that the final value computed matches the first. Given a legitimate “ring” formed through this method, anyone can verify that it indeed constitutes a “ring”, hence every value corresponds to the function computed on the previous value plus the specified seed, yet it remains impossible to discern at which “link” in the ring a private key was utilized.
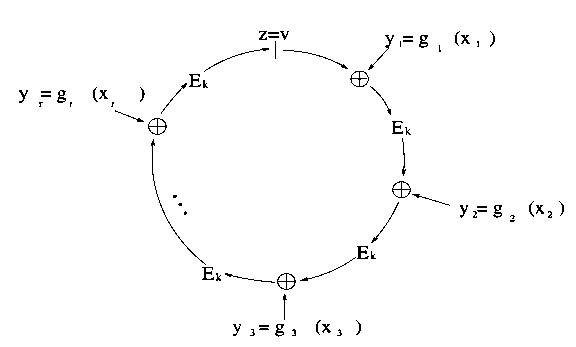
Moreover, there exists an enhanced variant of a ring signature known as a linkable ring signature, which introduces an additional characteristic: if you sign twice with the same private key, that instance can be detected – without disclosing any further information. For token anonymization, the application is rather straightforward: when a user intends to spend a coin, rather than asking them to furnish a conventional signature to demonstrate ownership of their public key directly, we aggregate public keys into groups and request that the user simply verify their membership in the group. Thanks to the linkability trait, a user possessing one public key in a group can only make a single transaction from that group; conflicting signatures are discarded.
Ring signatures may also find application in voting systems: instead of employing ring signatures to verify spending from a collection of coins, we utilize them to validate votes. They are also applicable for identity scenarios: if you wish to demonstrate that you belong to a collection of authorized users without revealing which one, ring signatures are particularly suitable for that purpose. Although ring signatures are more mathematically intricate than simple signatures, they are quite feasible to implement; some sample code for ring signatures built upon Ethereum can be located here.
Secret Sharing and Encryption
Occasionally, blockchain applications are not focused on mediating the transfer of digital assets, recording identity information, or managing smart contracts, but are rather applied to more data-centric uses: timestamping, high-value data storage, proof of existence (or proof of non-existence, as seen with certificate revocations), among others. A frequent saying is the notion of utilizing blockchains to construct systems where “users have control over their own data”.
In these situations, it is again crucial to emphasize that blockchains do NOT resolve privacy concerns and serve purely as an authenticity solution. Therefore, placing medical records in plaintext on a blockchain is a Very Poor Idea. However, they can be integrated with other technologies that do provide privacy, thereby crafting a comprehensive solution for numerous sectors that fulfills the required objectives, with blockchains functioning as a vendor-neutral platform where certain data can be housed to provide authenticity assurances.
What, then, are these privacy-enhancing technologies? Well, for basic data storage (e.g., medical records), we can utilize the most straightforward and oldest method of all: encryption! Documents stored as hashes on the blockchain can first be encrypted, ensuring that even if the data is saved on a platform like IPFS, only the individual with their private key can access the documents. If a user wishes to grant someone else the ability to view specific records in decrypted form, but not all of them, they can employ something like a deterministic wallet to generate a different key for each document.
Another valuable technology is secret sharing (discussed in greater detail here), which allows a user to encrypt a piece of data so that M out of N users (e.g., M = 5, N = 9) can collaborate to decrypt the data, but no fewer.
The Future of Privacy
There are two principal challenges associated with privacy-preserving protocols in blockchains. One challenge is statistical: for any privacy-protecting scheme to be computationally feasible, it must alter only a minor portion of the blockchain state with each transaction. However, even if the contents of the alteration are kept private, some amount of metadata will inevitably remain exposed. Thus, statistical examinations will always be able to discern something; at a minimum, they will likely be able to search for patterns of when transactions occur, and in many instances, they may be able to narrow down identities and ascertain who interacts with whom.
The second challenge relates to the developer experience. Turing-complete blockchains function exceptionally well for developers because they are highly accommodating to those who are entirely unacquainted with the underlying principles of decentralization: they create a decentralized “world computer” that resembles a centralized computer, effectively proclaiming, “look, developers, you can construct what you intended to build previously, except now this new layer at the base will magically make everything decentralized for you.” Of course, this abstraction is not flawless: elevated transaction fees, high latency, gas, and block reorganizations pose new challenges for programmers, but the barriers are not that significant.
In the realm of privacy, as we observe, there is no such magic bullet. While there exist partial solutions tailored for specific situations, and these often provide a considerable degree of flexibility, the abstractions they introduce are notably different from what developers are accustomed to. Transitioning from “10-line python script containing some instructions to subtract X coins from the sender’s balance and add X coins to the recipient’s balance” to “highly anonymized digital token utilizing linkable ring signatures” is not trivial.
Initiatives such as Hawk represent significant steps in a positive direction: they provide the potential to transform an arbitrary N-party protocol into a zero-knowledge-enabled protocol that depends solely on the blockchain for authenticity, and one specific party for privacy: essentially merging the advantages of both centralized and decentralized strategies. Can we extend this further and construct a protocol that relies on zero parties for privacy? This remains an active area of research, and we must await the developments to see how far we can progress.

