Among the fascinating challenges in crafting effective blockchain solutions is, how can we guarantee that these systems stay resistant to censorship? While significant efforts have been directed towards cryptoeconomics to ensure that blockchains consistently generate new blocks, and particularly to avert block reversion, considerably less focus has been given to the challenge of guaranteeing that transactions that individuals wish to integrate into the blockchain will indeed be processed, even if “the authorities”, at least concerning that specific blockchain, prefer otherwise.
Resistance to censorship in decentralized cryptoeconomic frameworks isn’t merely about ensuring that Wikileaks contributions or Silk Road 5.0 cannot be extinguished; it is fundamentally a crucial characteristic necessary for the secure functioning of a variety of financial protocols. To illustrate a straightforward yet high-value instance, consider contracts for difference. Imagine that participants A and B both invest 100 ETH into a contract wagering on the gold/USD exchange rate, stipulating that if the rate after 30 days is $1200, they both receive 100 ETH back, yet for every $1 the price rises, A receives an additional 1 ETH and B gets 1 ETH less. In the extremes, at $1000, B claims the whole 200 ETH, whereas at $1200, A garners the entire 200 ETH. To make this contract a valuable hedging instrument, an additional feature is necessary: if the price reaches $1190 or $1010 at any moment during those 30 days, the contract must process instantly, permitting both parties to withdraw their funds and enter into another contract to maintain the same exposure (the $10 margin serves as a safety buffer, allowing the parties to pull out and start a new contract without incurring any loss).
Now, suppose that the price climbs to $1195, and B wields the power to censor the network. In that case, B can hinder A from activating the force-liquidation clause. Such a significant price shift likely indicates more volatility ahead, suggesting that when the contract concludes, there is a 50% likelihood the price will revert to $1145 and a 50% likelihood it will escalate to $1245. Should the price return to $1145, then once the contract concludes, B incurs a loss of 45 ETH. However, if the price ascends to $1245, B only experiences a loss of 100 ETH due to the price adjustment of $145; consequently, B’s anticipated loss is merely 72.5 ETH rather than the 95 ETH it would incur if A had succeeded in activating the force-liquidation clause. Therefore, by obstructing A from broadcasting a transaction to the blockchain at that critical juncture, B has effectively achieved, in common economic and political terminology, the privatization of profits and the socialization of losses.
Additional instances comprise auditable computation, where the capacity to publish proof of wrongdoing within a designated timeframe is vital to the mechanism’s economic stability, decentralized exchanges, where censorship enables users to compel others to keep their exchange orders open longer than intended, and Schellingcoin-like protocols, where censors may enforce a specific outcome by censoring all votes that yield contrasting answers. Ultimately, in systems like Tendermint, consensus participants can employ censorship to obstruct other validators from joining the consensus pool, thereby solidifying the influence of their collusion. Thus, when everything is considered, anti-censorship is not merely about civil liberties; it centers on making it more difficult for consensus participants to partake in large-scale market manipulation schemes – an objective that appears to hold significant weight on the regulatory agenda.
What Is The Threat Model?
The initial inquiry to make is, what is the economic framework within which we are functioning? Who are the censors, what extent of power do they possess, and what is the cost incurred? We will divide this into two scenarios. In the first scenario, the censors lack sufficient power to independently block transactions; in the Tendermint scenario, this means the censors possess less than 33% of all validator positions, so they can certainly restrict transactions within their own blocks, but these transactions would merely be included in the subsequent block that does not censor them, and that block would still acquire its required 67% endorsements from the other nodes. In the second scenario, the censors hold enough power; in the context of Bitcoin, we can consider the top five mining companies and data centers colluding, and in the Tendermint situation, a coalition of very large stakeholders.
This may appear to be a trivial scenario to be concerned about – after all, many have argued that cryptoeconomic systems rest on a security assumption that such a large group of consensus participants cannot collude, and if they can, then we have already failed. Nonetheless, in those instances, we actually have a secondary layer of defense: such a collusion would devastate the underlying ecosystem and currency, hence being highly unprofitable for the involved parties. This argument isn’t flawless; we recognize that through bribery attacks, it is feasible for an attacker to orchestrate a collusion where non-participation is a public benefit, thus compelling all parties to participate even when it is collectively irrational, yet it still provides a robust defense against one of the most notable collusion avenues.
With historical reversion (i.e., 51% assaults), it is evident why executing such an attack would obliterate the ecosystem: it undermines literally the sole assurance that renders blockchains a fraction more effective than BitTorrent. However, concerning censorship, it isn’t as evident that the same scenario holds. One could potentially envision a circumstance in which a substantial group of stakeholders collude to first undermine specific highly objectionable types of transactions (e.g., child exploitation material, to reference a common fear used by censors and civil liberties advocates alike), and then progressively expand their control until it eventually falls into the hands of some ambitious newcomers who swiftly determine they can accrue billions through the cryptoeconomic equivalent of LIBOR manipulation. In the later phases, the censorship may be executed in such a meticulous and selective manner that it remains plausibly denied or even unnoticed.
Given the insights from Byzantine fault tolerance theory, there is no way to entirely prevent a collusion with over 33% participation in the consensus process from executing such actions. Nevertheless, what we can aim to achieve is one of two strategies:
- Render censorship costly.
- Render it impossible to censor specific items without outright censoring everything, or at the very least, without incapacitating a substantial portion of the protocol’s functionalities altogether.
Now, let’s explore some explicit methods inwhich we can execute individually.
Expense
The initial and most straightforward method to deter censorship is quite simple: rendering it unprofitable, or at least costly. Notably, proof of work does not meet this criterion: censorship is lucrative, for by censoring a block, one can (i) seize all of its transactions for personal gain, and (ii) ultimately claim its block reward, as the difficulty adjustment mechanism will lower difficulty to ensure that the block time stays at 10 minutes (or 15 seconds, or whichever) despite the miner being censored. Proof of stake mechanisms are also susceptible to (i) by default, but since we can monitor the total number of validators expected to be engaged, certain techniques can be implemented to make it less lucrative.
The most straightforward approach is to impose penalties on everyone for anyone’s lack of participation. If 100 out of 100 validators endorse a block, then all receive 100% of the reward. However, if only 99 validators endorse, then everyone receives 99% of the reward. Moreover, if a block is overlooked, all participants can face minor penalties for that as well. This leads to two sets of repercussions. Firstly, censoring blocks generated by others incurs costs for the censors. Secondly, the protocol can be structured such that if censorship occurs, altruistic individuals (i.e. standard software clients) can decline to approve the censoring blocks, thereby imposing additional costs on the censors. Naturally, some level of altruism is necessary for this cost strategy to have any impact – were there no altruistic individuals, then everyone would merely expect to be censored and not include any unwanted transactions from the start, but this assumption does increase overall costs significantly.
Timelock agreement
Regarding the second method, there are two main strategies that can be pursued. The first involves utilizing timelock puzzles, a form of encryption where a piece of data necessitates a specific duration to decrypt and which cannot be expedited through parallel processing. The conventional approach to timelock puzzles involves modular exponentiation; the core principle is to take a transaction d and create an encrypted value c with the characteristic:
If one knows p and q, then deriving c from d and retrieving d from c are both straightforward; apply the Chinese remainder theorem to break down the task into:
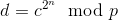
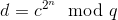
Subsequently, utilize Fermat’s little theorem for further decomposition into:
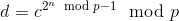
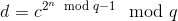
This can be achieved in a mere log(n) steps using two iterations of the square-and-multiply algorithm, one for the inner modular exponent and another for the outer modular exponent. One can apply the extended Euclidean algorithm to calculate modular inverses for executing this computation in reverse. However, without knowledge of p and q, an individual would need to literally multiply c by itself n times to reach the outcome – and, crucially,
- Sender generates transaction t
- Sender encrypts t using p and q to produce c, and transmits c and pq to a validator along with a zero-knowledge proof that the values were created accurately.
- The validator integrates c and pq into the blockchain
- A rule within the protocol mandates that the validator must input the correct original transaction t into the blockchain within 24 hours, failing which they risk losing a significant security deposit.
Honest validators would be inclined to participate as they know they will be able to decrypt the value in due time, yet they will remain unaware of what they are integrating into the blockchain until it’s too late. Typically, the sender will also submit t into the blockchain themselves as soon as c is integrated, aiming to expedite transaction processing; however, if the validators are dishonest, they will be compelled to submit it within 24 hours regardless. One could even amplify the process: a block is deemed invalid if there are still c values from over 24 hours ago that remain unintegrated.
This strategy bears the advantage that a gradual onset of censorship is outright impossible; it can only be full or absent. However, the “full” is still not remarkably extensive. The simplest evasion of the mechanism is for validators to merely collude and start demanding senders to forward t, p and q along with c, accompanied by a zero-knowledge proof verifying the accuracy of all the values. It would be a distinctly conspicuous and overt action, yet ultimately not a very costly one. An additional challenge of the approach is that it’s quite unnatural, necessitating a significant expenditure of computational power (not nearly as much as proof of work, but still requiring an hour’s worth of computational time on a single core) and somewhat atypical cryptography to achieve the goal. Therefore, one inquiry arises: is there a means by which we can improve upon this?
For a straightforward transaction processing system, the response is probably no, unless we develop enhanced versions of timelock that depend on network latency instead of computational power, perhaps inspired by Andrew Miller’s nonoutsourceable puzzles. However, for a Turing-complete object model, there are indeed some rather intriguing alternatives.
A crucial instrument in our toolkit is the halting problem: given a computer program, the only entirely dependable method to ascertain its actions after a series of execution steps is to actually execute it for that duration (note: the original formulation merely queries whether the program will halt, but the fundamental impossibility can be generalized across numerous output types and intermediate behaviors).
Within the context of Ethereum, this creates a distinctive denial-of-service attack vector: if a censor aims to obstruct transactions that yield an undesirable outcome (e.g., sending messages to or from a specific address), then that outcome could emerge after running for millions of computational steps, necessitating the censor to evaluate every transaction and eliminate those they wish to suppress. Typically, this is not an issue for Ethereum: as long as a transaction’s signature is valid, the transaction is well-structured, and sufficient ether is available to compensate for it, the transaction is assured to be legitimate and added to the blockchain, with the including miner guaranteed to receive a reward proportionate to the amount of computation that the transaction is permitted to occupy. In this instance, however, the censor is imposing an additional artificial validity condition, which cannot be verified nearly as “safely”.
Nevertheless, we cannot immediately conclude that this denial-of-service vulnerability will be detrimental: it may only take about a tenth of a second to verify a maximally sized transaction, and it is certainly possible to counteract attacks of that magnitude. Therefore, we need to progress further and introduce an upcoming Ethereum 1.1 feature: events. Events are a feature that enables a contract to generate a type of deferred message that is only activated at a predetermined block in the future. Once an event is triggered, any block at the height where the event is set to mature must execute the event to be valid. Consequently, transaction senders can be inventive and generate numerous transactions that create a multitude of events, whereby collectively, they produce an event that achieves a specific action that is not favored by censors.
Even at this stage, censors attempting to produce their blocks can still endeavor to simulate a sequence of empty blocks following the block they are generating, to determine if the series of events they are producing will result in any undesirable outcome. However, transaction senders can complicate matters significantly for censors: they can craft groups of transactions that generate events that do not independently achieve anything but do lead to the sender’s desired outcome in conjunction with some other transaction that occurs regularly (e.g., Bloomberg releasing some data feed into their blockchain contract). Depending on block timestamps or other unpredictable block data is another possibility. Note that this also complicates another defense mechanism against these anti-censorship strategies: insisting that transaction senders themselves provide a zero-knowledge proof that their transactions exhibit no undesirable intent.
To enhance the functionality of this framework, we can introduce another protocol feature: create a specialized address where messages directed to that address are executed as transactions. The messages would include the transaction data in a specific format (e.g., each message indicates one byte), with events triggered after several hundred blocks to amalgamate the data, which would then need to be promptly executed as a standard transaction; once the initial transactions are processed, there is no way to evade it. This would essentially guarantee that everything that can be accomplished by sending transactions (the primary input of the system) can be achieved through this type of covert latent messaging scheme.
Thus, we can observe how obstructing such circumventions will likely be exceptionally challenging to achieve completely and absolutely; rather, it will probably be a continuous two-sided battle of heuristics against heuristics where neither party would hold a permanent advantage. We may witness the rise of centralized firms whose sole role is to accept any transaction and discover a method to “sneak it in” to the blockchain in exchange for a fee, and these firms would consistently update their algorithms in response to the evolving algorithms of the entities trying to counteract their previous algorithms to block the attempts. Perhaps, this is the best course of action we can pursue.
Anti-censorship and Finality
It is vital to emphasize that the above by itself does not demonstrate that censorship is exceedingly costly all on its own. Rather, it indicates that if developers take care to incorporate certain features into the blockchain protocol, making censorship as challenging as reversion is feasible. This still raises the question of how daunting reversion is in the first instance. Numerous earlier consensus protocols, including proof of work
This, incidentally, serves as an important case study highlighting the significance of “bribe attacks” as a theoretical concern in cryptoeconomics: even though literal bribes may, in many instances, be impractical, external incentive modifications can arise from any source. If it can be demonstrated that blockchains are exceedingly costly to revert, then one can be certain that they will remain immensely costly to revert for

